由于对称矩阵的结构性质,其特征值问题在数值线性代数中有许多漂亮的算法.除![]() 迭代可以应用于对称特征值问题外,还有Jacobi迭代以及与SVD直接相关的三对角方法.
迭代可以应用于对称特征值问题外,还有Jacobi迭代以及与SVD直接相关的三对角方法.
 对称
对称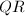 算法
算法
将![]() 迭代的思想结合矩阵的对称性质可以得到对称
迭代的思想结合矩阵的对称性质可以得到对称![]() 算法.其导出思路可以简述如下:
算法.其导出思路可以简述如下:
用于求最大特征值及特征向量的幂法和用于求不变子空间的![]() 迭代分别以
迭代分别以![]() 和
和![]() 的方式收敛到相应特征向量和不变子空间.这引导我们考虑
的方式收敛到相应特征向量和不变子空间.这引导我们考虑![]() 迭代,这相当于
迭代,这相当于![]() 的正交迭代.
的正交迭代.
我们考察对称![]() 迭代的加速算法.首先通过一系列Householder变换
迭代的加速算法.首先通过一系列Householder变换![]() 使得
使得![]() 是三对角阵,从而将之后每步迭代的运算量降至
是三对角阵,从而将之后每步迭代的运算量降至![]() 个flop,而三对角化这一步骤约需
个flop,而三对角化这一步骤约需![]() 个flop.其次,应用位移思想,可使收敛到对角形的速率为立方收敛.我们着重分析位移思想.
个flop.其次,应用位移思想,可使收敛到对角形的速率为立方收敛.我们着重分析位移思想.
若![]() 是一个近似特征值,则我们期望用位移
是一个近似特征值,则我们期望用位移![]() 进行一次
进行一次![]() 迭代后,
迭代后,![]() 元会很小.若
元会很小.若
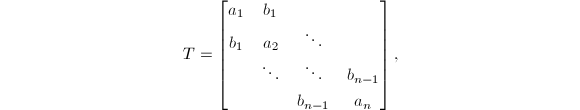 由Gerschgorin定理,位移的一个合理选择是
由Gerschgorin定理,位移的一个合理选择是![]() ,而一个更有效的选择是用
,而一个更有效的选择是用![]() 靠近
靠近![]() 的特征值作位移,这称为Wilkinson位移,它由
的特征值作位移,这称为Wilkinson位移,它由
![]() 给出,其中
给出,其中![]() .Wilkinson[1]证明了以上两种位移策略都是立方收敛,并给出了理由为什么更偏好后者.
.Wilkinson[1]证明了以上两种位移策略都是立方收敛,并给出了理由为什么更偏好后者.
应用隐式Q定理,不必显式形成矩阵![]() 就能实现从
就能实现从![]() 到
到![]() 的变换,这在
的变换,这在![]() 远大于某个
远大于某个![]() 时有优点.
时有优点.
首先取
![\begin{equation*}
G_1=G(1,2,\theta)=\left[
\begin{array}{cc|c}
c& s& \\
-s& c& \\\hline
& & I_{n-2}
\end{array}\right],
\end{equation*}](./latex/latex2png-SymmetricEigenvalueProblem_204782035_.gif) 使得
使得
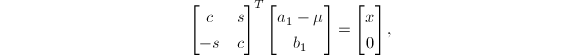 则
则
![]() 再计算
再计算![]() 使得
使得![]() 满足
满足![]() 且
且![]() 是三对角阵,就可以应用隐式Q定理.而实际中,我们使
是三对角阵,就可以应用隐式Q定理.而实际中,我们使
![]() 则
则![]() 和
和![]() 的第一列相等且
的第一列相等且![]() 可用于将多余的非零元素逐出矩阵
可用于将多余的非零元素逐出矩阵![]() .这样就完成了
.这样就完成了![]() 到
到![]() 的变换,从而完成了对称
的变换,从而完成了对称![]() 算法的一个步骤.
算法的一个步骤.
 Jacobi方法
Jacobi方法
求解对称特征值问题的Jacobi迭代法因易于并行化而引起人们的注意.它通过进行一系列正交相似变换
![]() 逐步减小
逐步减小
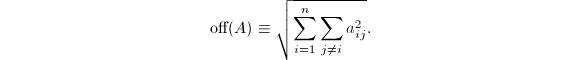 我们可以形象地称
我们可以形象地称![]() 为非对角元素的Frobenius范数.实现它的工具是Jacobi-Givens旋转变换.
为非对角元素的Frobenius范数.实现它的工具是Jacobi-Givens旋转变换.
Jacobi方法的基本步骤:
- 选择指标
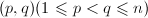 ,在经典Jacobi算法中选择
,在经典Jacobi算法中选择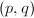 使
使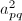 最大.
最大. - 计算一个余弦-正弦对
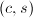 ,使得
,使得
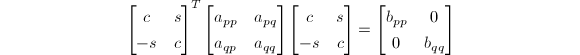 为对角阵.
为对角阵. - 令
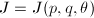 ,计算
,计算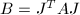 并覆盖
并覆盖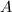 .
.
容易得到,经过一次Jacobi步骤后,
![]() 在此意义下,每个Jacobi步骤后
在此意义下,每个Jacobi步骤后![]() 更"靠近"对角形.
更"靠近"对角形.
经典Jacobi方法(选取![]() 最大)的每次校正要做
最大)的每次校正要做![]() 次运算,但选取最大元素却需
次运算,但选取最大元素却需![]() 次比较.解决此矛盾的途径是将变换顺序固定下来,如逐行进行"扫描",这称为行循环方法,它是二次收敛的.作为对比,
次比较.解决此矛盾的途径是将变换顺序固定下来,如逐行进行"扫描",这称为行循环方法,它是二次收敛的.作为对比,![]() 算法是立方收敛的.
算法是立方收敛的.
如前所述,Jacobi方法的优势在于其并行本性.事实上,Jacobi旋转![]() 只作用于
只作用于![]() ,
,![]() 行和
行和![]() ,
,![]() 列.这样,每次将矩阵的全部行与列划分为若干互不冲突的组,每组的运算可以得到并行的处理.各族变换并行处理完成后,变换行与列的划分(类似一次循环赛的过程),直至所有
列.这样,每次将矩阵的全部行与列划分为若干互不冲突的组,每组的运算可以得到并行的处理.各族变换并行处理完成后,变换行与列的划分(类似一次循环赛的过程),直至所有![]() 对都得到处理.这种并行的思想也同样适用于分块的Jacobi迭代.
对都得到处理.这种并行的思想也同样适用于分块的Jacobi迭代.
 对称三对角矩阵的特征值方法
对称三对角矩阵的特征值方法
 Sturm序列与二分法
Sturm序列与二分法
令![]() 表示
表示![]() 的
的![]() 阶顺序主子阵,定义其特征多项式
阶顺序主子阵,定义其特征多项式![]() ,则有以下递推公式(设
,则有以下递推公式(设![]() ):
):
![]() 因通过
因通过![]() 次运算即可计算
次运算即可计算![]() 的值,故利用二分法找它的根是可行的.显然,二分迭代是线性收敛,即每步将误差减半.
的值,故利用二分法找它的根是可行的.显然,二分迭代是线性收敛,即每步将误差减半.
对于不可约三对角阵,有如下经典结果,其证明可参见[2].
结合Gerschgorin定理可知![]() .其中
.其中![]() ,
,![]() .于是我们可以此为初始值,进行二分法迭代,每次迭代的判断条件为
.于是我们可以此为初始值,进行二分法迭代,每次迭代的判断条件为![]() ,则可求出
,则可求出![]() 的第
的第![]() 大的特征值.
大的特征值.
与![]() 迭代相比,对分法的优势在于无论特征值大小,计算值都具有小的相对误差.
迭代相比,对分法的优势在于无论特征值大小,计算值都具有小的相对误差.
 分而治之方法
分而治之方法
适合于并行处理的三对角阵特征值算法是以以下观察为基础的:设![]() ,定义
,定义
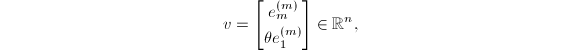 则
则
![]() 除了"中间四个"元素
除了"中间四个"元素
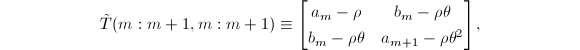
![]() 与
与![]() 相等.若取
相等.若取![]() ,则
,则
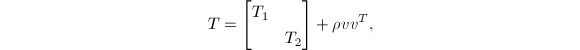 其中,
其中,
 这样,我们就把
这样,我们就把![]() "撕"成了两片,并加上一个修正项.分别解决
"撕"成了两片,并加上一个修正项.分别解决![]() ,
,![]() 的特征值问题
的特征值问题
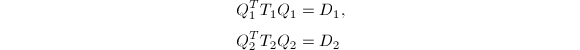 后,只要快速求解一个对角矩阵向量外积修正的特征值问题
后,只要快速求解一个对角矩阵向量外积修正的特征值问题
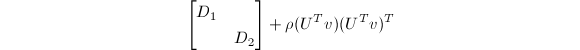 就可以了.
就可以了.
对角矩阵向量外积修正的特征值问题的主要计算依赖于以下结果:
上述定理表明要计算![]() ,我们应首先用Newton型算法找出
,我们应首先用Newton型算法找出![]() 的根
的根![]() ,然后对
,然后对![]() ,通过正规化向量
,通过正规化向量![]() 来计算
来计算![]() 的列向量.
的列向量.
以下考察有重复的![]() 或零分量
或零分量![]() 的情形,我们对以下定理给出一个构造性的证明,从而解决问题:
的情形,我们对以下定理给出一个构造性的证明,从而解决问题:
- 假设对某个
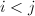 有
有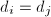 ,令
,令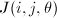 是
是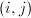 平面上的旋转变换,使
平面上的旋转变换,使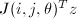 的第
的第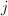 个分量为
个分量为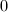 .易知
.易知
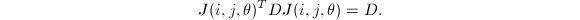 于是,若有一个重复的
于是,若有一个重复的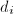 ,我们就能使
,我们就能使 的一个分量化为
的一个分量化为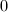 .
. - 令
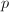 是
是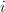 和
和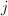 列互换的单位阵,可推出
列互换的单位阵,可推出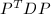 是对角阵,这样我们就可将为零的
是对角阵,这样我们就可将为零的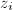 放在底部.重复以上步骤就可得到所需的标准结构.
放在底部.重复以上步骤就可得到所需的标准结构.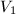 是这些旋转阵之积.
□
是这些旋转阵之积.
□
综合上述所述,我们就得到了分而治之算法.
 计算SVD
计算SVD
矩阵![]() 的奇异值分解与对称阵
的奇异值分解与对称阵![]() ,
,![]() 的Schur分解有着密切的联系.若
的Schur分解有着密切的联系.若![]() 是
是![]() 的SVD,则
的SVD,则
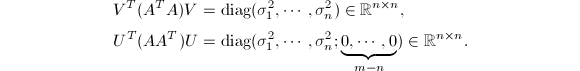
我们计算![]() 的SVD的思路就是将其化为
的SVD的思路就是将其化为![]() 的Schur分解来进行.但如果显式形成
的Schur分解来进行.但如果显式形成![]() ,则可能造成信息的损失.Golub和Kahan (1965)[3]给出了基于隐式对称
,则可能造成信息的损失.Golub和Kahan (1965)[3]给出了基于隐式对称![]() 算法的SVD方法.
算法的SVD方法.
首先用Householder变化将![]() 化为双对角形:
化为双对角形:
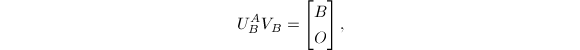 其中
其中
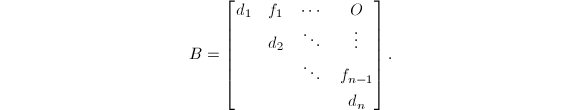 接下来只要计算
接下来只要计算![]() 的SVD.为此考虑三对角阵
的SVD.为此考虑三对角阵![]() ,应用
,应用![]() 算法:
算法:
- 计算矩阵
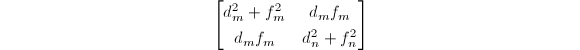 (其中
(其中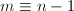 )的靠近
)的靠近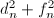 的特征值
的特征值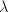 .
. - 计算
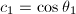 和
和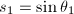 使得
使得
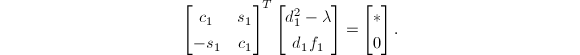 令
令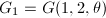 .
. - 计算Givens旋转
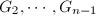 ,使得当
,使得当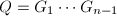 时,
时,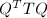 为三对角阵,且
为三对角阵,且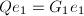 .
.
正如之前指出的,以上算法需显式计算![]() ,这可能导致算法的不稳定.若我们把Givens变化
,这可能导致算法的不稳定.若我们把Givens变化![]() 直接作用到
直接作用到![]() 上,在决定Givens旋转
上,在决定Givens旋转![]() 将
将![]() 恢复为双对角阵,得到
恢复为双对角阵,得到
![]() 由
由![]() 的形式可知
的形式可知
![]() 从而由隐式Q定理断言
从而由隐式Q定理断言![]() 和
和![]() 本质相同.于是我们隐式地完成了
本质相同.于是我们隐式地完成了![]() 到
到![]() 的过程.
的过程.
由于以上本质上是对称![]() 迭代的方法,所以其收敛是三次的.实际中我们通过检测
迭代的方法,所以其收敛是三次的.实际中我们通过检测![]() 的小次对角元来决定何时将问题降阶或终止迭代.
的小次对角元来决定何时将问题降阶或终止迭代.
Chan (1982)[4]对Golub和Kahan的算法进行了改进.通过合理安排运算顺序,在![]() 时可以有效地减少运算量.
时可以有效地减少运算量.
- 形成双对角矩阵时,先通过Householder变换,将
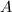 上三角化:
上三角化:
![\begin{equation*}
L^TA=
\begin{bmatrix}
R\\
O
\end{bmatrix}
\begin{array}[c]{l}
n\\
m-n
\end{array},
\end{equation*}](./latex/latex2png-SymmetricEigenvalueProblem_241834059_.gif) 其中
其中 为上三角阵.随后利用
为上三角阵.随后利用 的上三角性质,利用Givens变换或快速Givens变换将其化为双对角形.由于R-双对角化时只需对较短的向量进行操作,而Givens变换较Householder变换可以减少加法的数目,特别在不需要求变换矩阵时可以有效地减少运算量.当
的上三角性质,利用Givens变换或快速Givens变换将其化为双对角形.由于R-双对角化时只需对较短的向量进行操作,而Givens变换较Householder变换可以减少加法的数目,特别在不需要求变换矩阵时可以有效地减少运算量.当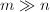 时尤其有效.
时尤其有效. - 当求得
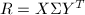 之后,SVD的变换矩阵可如下求出:
之后,SVD的变换矩阵可如下求出:
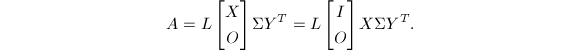
Chan给出了算法复杂度的详细分析.他指出在![]() 时,R-双对角化几乎总是比Golub-Kahan算法更快速,特别在不需显式求出变换矩阵的情况下.
时,R-双对角化几乎总是比Golub-Kahan算法更快速,特别在不需显式求出变换矩阵的情况下.
设我们已求得![]() 矩阵
矩阵![]() 的奇异值
的奇异值![]() ,来考虑如何求正交矩阵
,来考虑如何求正交矩阵![]() ,
,![]() ,使
,使![]() ,其中
,其中![]() .
.
事实上,我们已求得![]() 的特征值
的特征值![]() ,要求正交矩阵
,要求正交矩阵![]() ,其列向量是
,其列向量是![]() 的特征向量,我们只要用逆迭代求解
的特征向量,我们只要用逆迭代求解![]() .实用中采用双对角矩阵
.实用中采用双对角矩阵![]() 代替
代替![]() ,之后令
,之后令![]() 的相应列
的相应列![]() 即可.这些算法都是稳定有效的.
即可.这些算法都是稳定有效的.
参考文献
[1]Global Convergence of Tridiagonal QR Algorithm With Origin Shifts, Lin. Alg. and Its Applic. I (1968), 409-420.
[2]The Algebraic Eigenvalue Problem, Clarendon Press, Oxford, UK, 1965.
[3]Calculating the Singular Values and Pseudo-Inverse of a Matrix, SIAM J. Num. Anal. Ser. B 2 (1965), 205-224.
[4]An Improved Algorithm for Computing the Singular Value Decomposition, ACM Trans. Math. Soft. 8 (1982), no.1, 72-83.