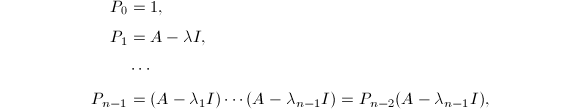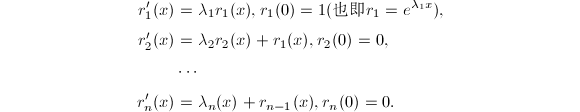特征值方法
特征值方法
给定一![]() 阶方阵
阶方阵![]() 和标量函数
和标量函数![]() ,有多种方法定义矩阵
,有多种方法定义矩阵![]() .例如,对于
.例如,对于![]() 及
及![]() ,可分别用
,可分别用![]() 及Taylor级数
及Taylor级数![]() 来定义.一种较精确而广泛的定义利用线积分:假设
来定义.一种较精确而广泛的定义利用线积分:假设![]() 在闭曲线
在闭曲线![]() 的内部解析,且
的内部解析,且![]() 包围了
包围了![]() ,则定义
,则定义![]() 为
为
![]()
以上定义可以用来导出![]() 的一些实际特性.例如,若
的一些实际特性.例如,若![]() 有定义,且
有定义,且![]() ,则
,则![]() 特别地,当
特别地,当![]() 为Jordan块时,可有如下结果:
为Jordan块时,可有如下结果:
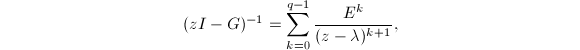 由Cauchy积分定理可知
由Cauchy积分定理可知
![\begin{equation*}
f (G)=\sum\limits_{k=0}^{q-1}\left[\frac{1}{2\pi i}\oint_\Gamma \frac{f(z)}{(z-\lambda)^{k+1}}\mathrm{d}z\right]E^k=\sum\limits_{k=0}^{q-1}\frac{f^{(k)} (\lambda)}{k!}E^k.
\end{equation*}](./latex/latex2png-MatrixFunction_264466002_.gif) 注意到
注意到以上结果给出了![]() 与
与![]() 的特征系统之间的密切联系,但除非
的特征系统之间的密切联系,但除非![]() 能被良态矩阵
能被良态矩阵![]() 对角化,用Jordan标准型处理矩阵函数的数值特性不可靠.
对角化,用Jordan标准型处理矩阵函数的数值特性不可靠.
利用Schur分解可避免Jordan分解带来的困难.若![]() 是
是![]() 的Schur分解,则
的Schur分解,则![]() .因此,我们需要一个计算上三角阵函数的算法,但因为
.因此,我们需要一个计算上三角阵函数的算法,但因为![]() 的显式表示极其复杂.我们代之以下的算法 (Parlett,1974),用以计算
的显式表示极其复杂.我们代之以下的算法 (Parlett,1974),用以计算![]() 的严格上三角部分,它仅需
的严格上三角部分,它仅需![]() 个flop.
个flop.
由![]() ,比较方程两边的
,比较方程两边的![]() 元可知
元可知![]() 若
若![]() ,则
,则
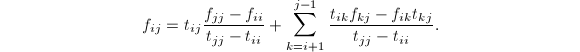 由此,在已知对角元
由此,在已知对角元![]() 后,可逐对角线地递推出
后,可逐对角线地递推出![]() 的整个严格上三角部分.
的整个严格上三角部分.
但是,以上算法在矩阵![]() 有邻近的重特征值时失效.此时可采用其分块形式 (Parlett,1974).第一步在Schur分解中选取恰当的
有邻近的重特征值时失效.此时可采用其分块形式 (Parlett,1974).第一步在Schur分解中选取恰当的![]() 使得
使得![]() 的相同或相近特征值集中在
的相同或相近特征值集中在![]() 的对角块
的对角块![]() 中,也即计算分划
中,也即计算分划
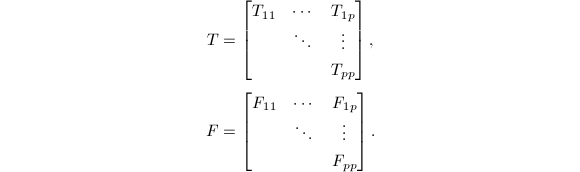 其中
其中![]() 用特征值排序的算法可以做到这一点.
用特征值排序的算法可以做到这一点.
下一步计算子矩阵![]() ,这将用以后阐述的方法.一旦
,这将用以后阐述的方法.一旦![]() 的对角块已知,
的对角块已知,![]() 的严格上三角块也可如下递推算出.仍然比较
的严格上三角块也可如下递推算出.仍然比较![]() 中
中![]() 的块,则
的块,则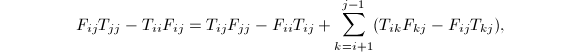 每次要算出
每次要算出![]() 的一条块对角线,它可以用之前介绍的Bartels-Stewart算法求解.
的一条块对角线,它可以用之前介绍的Bartels-Stewart算法求解.
 逼近算法
逼近算法
在数值计算中,可采用逼近法.其基本思想是若![]() 在
在![]() 上逼近
上逼近![]() ,则
,则![]() 逼近
逼近![]() .一个逼近矩阵函数的常用方法是Taylor级数,而针对具体函数形式则有更多更好的选择,如
.一个逼近矩阵函数的常用方法是Taylor级数,而针对具体函数形式则有更多更好的选择,如![]() 可用Pad\'{e}函数逼近.
可用Pad\'{e}函数逼近.
逼近法中常需计算矩阵的多项式.设![]() ,最明显的办法是采用Horner的技巧,它需要
,最明显的办法是采用Horner的技巧,它需要![]() 矩阵乘法:
矩阵乘法:![]() .但由于矩阵乘法与数乘性质不同,故更常用以下的算法:
.但由于矩阵乘法与数乘性质不同,故更常用以下的算法:
设![]() 为满足
为满足![]() 的整数,则
的整数,则![]() 其中
其中
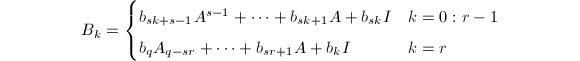 只要计算出
只要计算出![]() ,则Horner规则即可应用于上式.
,则Horner规则即可应用于上式.![]() 的结果可只用
的结果可只用![]() 次矩阵乘法得到.取
次矩阵乘法得到.取![]() 时,乘法次数大致最少.
时,乘法次数大致最少.
以上计算中,矩阵求幂可采用所谓二进制求幂法.即先计算![]() 为
为![]() 的二次幂的展开
的二次幂的展开![]() ,分别计算
,分别计算![]() 将其累积出
将其累积出![]() .这一算法最多需要
.这一算法最多需要![]() 次矩阵乘法,若
次矩阵乘法,若![]() 是
是![]() 的幂,则只要
的幂,则只要![]() 次矩阵乘法.
次矩阵乘法.
 矩阵指数
矩阵指数
经常要计算的矩阵函数之一是指数![]() 计算它的算法有许多,但正如Moler和Van Loan (1978,2003)[1]的综述文章所指出的,它们中的大多数是不可靠的.以下介绍两种算法,它们分别适用于数值计算和精确计算.
计算它的算法有许多,但正如Moler和Van Loan (1978,2003)[1]的综述文章所指出的,它们中的大多数是不可靠的.以下介绍两种算法,它们分别适用于数值计算和精确计算.
 Pad\'{e}逼近
Pad\'{e}逼近
考虑如下一类逼近函数,Pad\'{e}函数:![]() 其中,
其中,
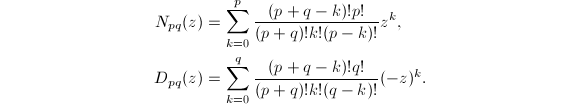
但Pad\'{e}逼近仅在原点才有效.但利用![]() 可克服这一困难.特别地,若取
可克服这一困难.特别地,若取![]() ,则可使求幂的计算十分有效地进行,而整个逼近的好坏取决于
,则可使求幂的计算十分有效地进行,而整个逼近的好坏取决于![]() 的精度.Moler和Van Loan(1978)证明了,若
的精度.Moler和Van Loan(1978)证明了,若![]() 则存在扰动矩阵
则存在扰动矩阵![]() 满足
满足
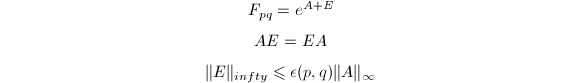 其中,
其中,![]() 由此可以导出Pad\'{e}逼近的精度估计:
由此可以导出Pad\'{e}逼近的精度估计:
![]() 参数
参数![]() 可根据要求的相对误差来确定.注意到
可根据要求的相对误差来确定.注意到![]() 大约需要
大约需要![]() 次矩阵乘法,故通常令
次矩阵乘法,故通常令![]() ,这样就得到以下算法:
,这样就得到以下算法:
这一算法大约需要![]() 个flop,其中特殊的Horner技巧可用于加快
个flop,其中特殊的Horner技巧可用于加快![]() 和
和![]() 的计算.相比同样精度的Taylor逼近,Pad\'{e}逼近要减少约一半的计算量.
的计算.相比同样精度的Taylor逼近,Pad\'{e}逼近要减少约一半的计算量.
 Putzer方法
Putzer方法
若已知矩阵![]() 的特征值 (在精确计算中借助其特征多项式得到),则关于矩阵指数
的特征值 (在精确计算中借助其特征多项式得到),则关于矩阵指数![]() 有如下定理[2],它给出了一种精确计算矩阵指数的方法:
有如下定理[2],它给出了一种精确计算矩阵指数的方法:
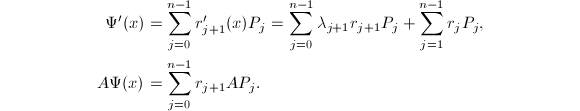 由
由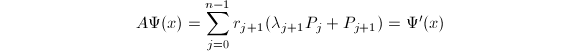 □
□
 为
为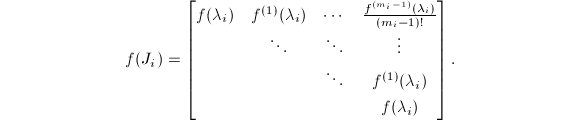
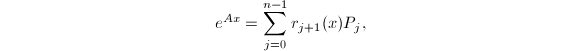 其中,
其中,