 有理函数积分
有理函数积分
 部分分式分解
部分分式分解
最简单的多项式函数无需赘言,因此我们首先考虑有理函数![]() 的符号积分,其中
的符号积分,其中![]() ,满足
,满足![]() ,不失一般性还可假设
,不失一般性还可假设![]() 。最朴素的办法是利用部分分式分解。
。最朴素的办法是利用部分分式分解。
设![]() ,反复利用引理1则有
,反复利用引理1则有![]() 其中
其中![]() 。再将
。再将![]() 在
在![]() 处展开可得
处展开可得![]() 其中
其中![]() 为常数。于是得到
为常数。于是得到
![]()
有理函数符号积分的问题在理论上解决了,即所有有理函数的积分均可由有理函数和对数函数表示,分别称为积分的有理部分和对数部分。但还有几个不得不处理的问题:一方面需要在![]() 上完全分解
上完全分解![]() ,而精确地做到这一点并不总那么容易,另一方面我们更希望看到的是,在算法的计算中除了用于表示最终积分的数以外,不要出现其他系数域扩域中的代数数。
,而精确地做到这一点并不总那么容易,另一方面我们更希望看到的是,在算法的计算中除了用于表示最终积分的数以外,不要出现其他系数域扩域中的代数数。
 Hermite方法
Hermite方法
Hermite方法使用多项式的无平方分解来代替完全分解,而无平方分解可以在系数域中完成。设![]() 的无平方分解为
的无平方分解为![]() ,其中
,其中![]() 无平方因子且两两互素。从而
无平方因子且两两互素。从而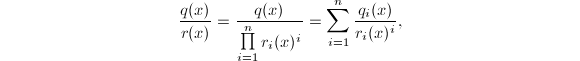 其中
其中![]() 。因此我们只需要考虑积分
。因此我们只需要考虑积分![]() 即可。
即可。
由于![]() 无平方因子,故
无平方因子,故![]() ,可设
,可设![]() ,代入进行分部积分
,代入进行分部积分
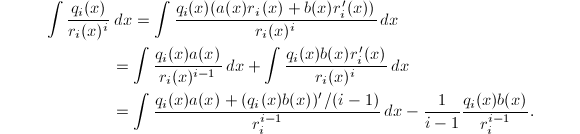 为了简便起见,我们将省略变元
为了简便起见,我们将省略变元![]() 与记号
与记号![]() ,以下的积分与导数总是对
,以下的积分与导数总是对![]() 而言的,例如上式即可简写为
而言的,例如上式即可简写为
![]()
此过程称为Hermite约化过程。通过一次分部积分,被积函数分母中![]() 的次数便降低一次,如此续行即可完全得到积分的有理部分。
的次数便降低一次,如此续行即可完全得到积分的有理部分。
 Horowitz-Ostrogradsky方法
Horowitz-Ostrogradsky方法
Hermite方法避免了完全分解,但仍要求无平方分解和关于![]() 的部分分式分解。Horowitz-Ostrogradsky方法则不需要其他工具,通过待定系数法将问题归结为线性方程的求解问题。
的部分分式分解。Horowitz-Ostrogradsky方法则不需要其他工具,通过待定系数法将问题归结为线性方程的求解问题。
设![]() 其中
其中![]() 为积分的有理部分,由部分分式的结果可知
为积分的有理部分,由部分分式的结果可知![]() ,
,![]() 。求导得到
。求导得到
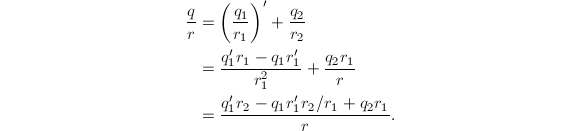 从而问题归结为求
从而问题归结为求![]() ,
,![]() 满足
满足![]() 且
且![]() ,
,![]() 。以
。以![]() ,
,![]() 的系数作为未知变量,这是一个至多
的系数作为未知变量,这是一个至多![]() 维的线性方程组问题。
维的线性方程组问题。
 Rothstein-Trager方法
Rothstein-Trager方法
下面的问题是如何求出对数部分,因此我们设![]() 无平方因子的首一多项式,并可设
无平方因子的首一多项式,并可设![]() 其中
其中![]() 为互不相同的常数,
为互不相同的常数,![]() 为无平方因子的首一多项式,两两互素(可以通过合并项来满足这些条件)。求导得到
为无平方因子的首一多项式,两两互素(可以通过合并项来满足这些条件)。求导得到![]() 由于
由于![]() 无平方因子且两两互素可知
无平方因子且两两互素可知![]() 记
记![]() ,则有
,则有![]() 及
及![]() 于是对于
于是对于![]()
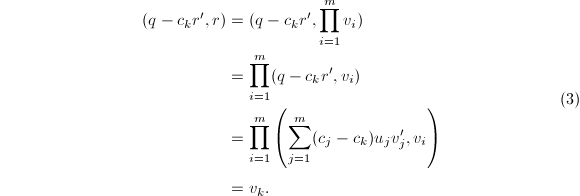 最后一个等式成立是因为
最后一个等式成立是因为
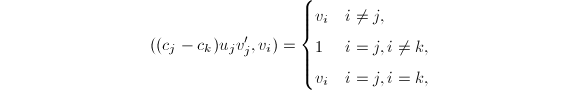 从而
从而
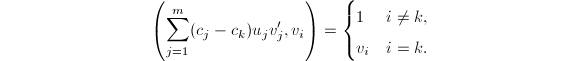
由式(3)可以看出,当我们找出系数![]() 后即可通过最大公因子的计算求出
后即可通过最大公因子的计算求出![]() 。如何求出
。如何求出![]() 呢?同样的论证可以知道
呢?同样的论证可以知道![]() ,而
,而![]() (此结式称为Rothstein-Trager结式),故求解关于
(此结式称为Rothstein-Trager结式),故求解关于![]() 的方程
的方程![]() 即可得到所有的系数
即可得到所有的系数![]() 。
。
 Lazard-Rioboo-Trager方法
Lazard-Rioboo-Trager方法
Rothstein-Trager方法解决了引入不必要扩张常数的问题,但仍需要计算许多代数数域上多项式的最大公因子,Lazard-Rioboo-Trager方法是对此的一个改进,只需要无平方分解和若干带余除法即可。
设![]() ,
,![]() ,由结式的性质得到
,由结式的性质得到![]() 其中
其中![]() 为非零常数。从而
为非零常数。从而![]() 中
中![]() 的重数为满足
的重数为满足![]() 的
的![]() 的个数。而
的个数。而
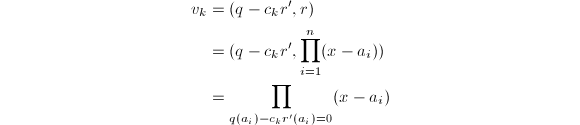 可知
可知![]() 等于
等于![]() 中
中![]() 的重数。由此出发可知:设被积函数的系数域为
的重数。由此出发可知:设被积函数的系数域为![]() ,则只需要在
,则只需要在![]() 中对
中对![]() 和
和![]() 做Euclid除法,设
做Euclid除法,设![]() 为余式序列中关于
为余式序列中关于![]() 次数为
次数为![]() 的多项式,则有
的多项式,则有![]() 。另外,如果用多项式余式序列(PRS)算法来计算结式
。另外,如果用多项式余式序列(PRS)算法来计算结式![]() 的话,
的话,![]() 的计算可以与结式的计算同时进行。
的计算可以与结式的计算同时进行。
 Liouville定理
Liouville定理
从直观上来看,所有有理函数总是可以积出。这里“积出”的精确含义是,可以找到一个初等函数作为被积函数的原函数。为了将问题的本质看得更清楚,我们引入如下定义。
容易验证微分代数的基本性质使得我们可以完全脱离分析语言,将符号积分的问题视为纯代数问题。而我们关心的“初等函数”,也可以直接用代数语言来描述。
 在
在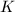 上是代数的,即有
上是代数的,即有![$f(x)\in K[x]$](./latex/latex2png-Integration_40994369_-5.gif) 使得
使得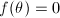 ;
;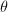 在
在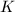 上是指数的,即有
上是指数的,即有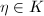 使得
使得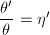 (记
(记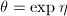 );
);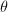 在
在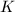 上是对数的,即有
上是对数的,即有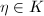 使得
使得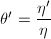 (记
(记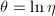 )。
)。
称![]() 为
为![]() 上的一个初等函数域,若
上的一个初等函数域,若![]() ,
,![]() 为
为![]() 上的初等生成元。任
上的初等生成元。任![]() 上的一个初等函数域中的元素称为
上的一个初等函数域中的元素称为![]() 上的初等函数。
上的初等函数。
下面来自Liouville的重要定理,描述了积分为初等函数时必定具有的形式,证明需要对三种特殊扩张情形进行讨论,并最终得出一般情形[4],[2]。
 超越对数函数积分
超越对数函数积分
 分解引理
分解引理
设![]() 为
为![]() 上的一个超越对数函数,我们考虑
上的一个超越对数函数,我们考虑![]() 的积分问题。可设
的积分问题。可设![]() ,其中
,其中![]() ,
,![]() ,
,![]() 互素且
互素且![]() ,下面的引理使得我们能够沿着和有理函数积分类似的道路走下去。
,下面的引理使得我们能够沿着和有理函数积分类似的道路走下去。
![\begin{align*}
p+\frac{q}{r}&=\left(p_0+\dfrac{q_0}{r_0}\right)'+\sum_{i=1}^kc_i\frac{v_i'}{v_i}+\sum_{i=k+1}^nc_i\frac{v_i'}{v_i} \\
&=\underbrace{\left(p_0'+\sum_{i=1}^kc_i\frac{v_i'}{v_i}\right)}_{\in \hat K[\theta]}+\underbrace{\left(\left(\frac{q_0}{r_0}\right)'+\sum_{i=k+1}^nc_i\frac{v_i'}{v_i}\right)}_{\in \hat K(\theta)\text{为真分式}}.
\end{align*}](./latex/latex2png-Integration_262502375_.gif) 由于
由于由于![]() 在
在![]() 上超越,等式两端的关于
上超越,等式两端的关于![]() 的多项式和真分式必定对应相等,从而
的多项式和真分式必定对应相等,从而
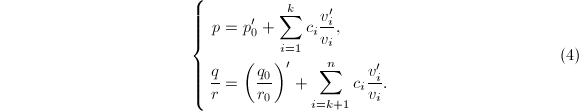 故
故![]() ,
,![]() 都在
都在![]() 上有初等积分。
□
上有初等积分。
□
 多项式部分
多项式部分
由分解引理,我们可以等价地分别对多项式部分![]() 和有理部分
和有理部分![]() 分别求积分,如果其中有一个无初等积分,则
分别求积分,如果其中有一个无初等积分,则![]() 也必无初等积分。
也必无初等积分。
在式(4)中设![]() 其中
其中![]() ,则有
,则有![]() 由于
由于![]() 已知,我们的目标是求出
已知,我们的目标是求出![]() 和
和![]() 。利用
。利用![]() 在
在![]() 上超越,可得
上超越,可得
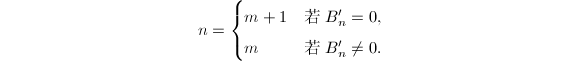 若
若![]() ,则
,则![]() 为非零常数,否则可约定
为非零常数,否则可约定![]() ,于是无论何种情况考虑
,于是无论何种情况考虑![]() 的最高次项
的最高次项![]() 可得
可得![]() 所以
所以![]() 可知
可知![]() 为
为![]() 中小于一次的多项式,可确定下常数
中小于一次的多项式,可确定下常数![]() 以及
以及![]() 。当然,由于
。当然,由于![]() 积分常数的存在,
积分常数的存在,![]() 的确定是在相差一个常数下而言的,设此积分常数为
的确定是在相差一个常数下而言的,设此积分常数为![]() 。接下来再考虑两边
。接下来再考虑两边![]() 项可得
项可得![]() 同样可知
同样可知![]() 于是
于是![]() 为
为![]() 中小于一次的多项式,可确定常数
中小于一次的多项式,可确定常数![]() 及
及![]() (
(![]() 为积分常数)。如此续行,直到比较
为积分常数)。如此续行,直到比较![]() 项可得
项可得![]() 积分得
积分得![]() 最终求出常数
最终求出常数![]() ,以及
,以及![]() 上的对数部分
上的对数部分![]() (注意这最后一步右端积分未必落在
(注意这最后一步右端积分未必落在![]() 中),从而我们(在相差一个常数的意义下)求出了多项式部分的积分。
中),从而我们(在相差一个常数的意义下)求出了多项式部分的积分。
 有理部分与对数部分
有理部分与对数部分
我们希望求出(4)中的![]() 和
和![]() ,求积分的有理部分和对数部分可以和有理函数积分类似的做。为确保类似Hermite约化的过程能够进行,我们验证如下的引理。
,求积分的有理部分和对数部分可以和有理函数积分类似的做。为确保类似Hermite约化的过程能够进行,我们验证如下的引理。
 若
若有了引理3中![]() 的保证,我们就可以施行Hermite约化过程了。将
的保证,我们就可以施行Hermite约化过程了。将![]() 在
在![]() 上作无平方分解
上作无平方分解![]() ,完全类似可以得到式(2)的约化结果,从而求出积分的有理部分
,完全类似可以得到式(2)的约化结果,从而求出积分的有理部分![]() 。
。
同样有求对数部分的Rothstein-Trager方法的类似版本。设![]() 无平方因子,则积分的形式必为
无平方因子,则积分的形式必为![]() ,其中
,其中![]() 为常数,
为常数,![]() 。求得Rothstein-Trager结式
。求得Rothstein-Trager结式![]() 关于
关于![]() 的根
的根![]() ,若有
,若有![]() 不是常数,则
不是常数,则![]() 在
在![]() 上必无初等积分;若
上必无初等积分;若![]() 均为常数,计算最大公因子
均为常数,计算最大公因子![]() 即可得到
即可得到![]() 。
。
 超越指数函数积分
超越指数函数积分
我们沿着有理函数积分的道路顺利地解决了超越对数函数积分的问题,接下来自然要考虑的是超越指数函数积分了,即![]() 为
为![]() 上的超越指数函数,
上的超越指数函数,![]() 的积分问题。
的积分问题。
但这个问题变得要复杂一些,一方面在计算过程中我们需要在基域![]() 中求解微分方程(被称为Risch微分方程[5])
中求解微分方程(被称为Risch微分方程[5])![]() 其中
其中![]() ,
,![]() 为未知函数。我们将在微分方程符号解中专门讨论Risch微分方程,而且将看到Risch微分方程和符号积分在某种意义下的相互“纠缠”。现在我们暂时假设已经能够在
为未知函数。我们将在微分方程符号解中专门讨论Risch微分方程,而且将看到Risch微分方程和符号积分在某种意义下的相互“纠缠”。现在我们暂时假设已经能够在![]() 上完成这样的求解。
上完成这样的求解。
复杂性的另一面在于,![]() 无平方因子也不能保证
无平方因子也不能保证![]() 。
。
因此我们需要对引理3做一个小的修订。
设![]() 为
为![]() 在
在![]() 上的分解。则由复合函数求导
上的分解。则由复合函数求导
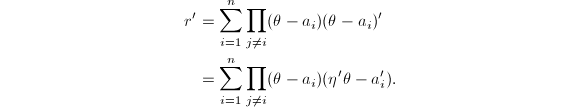 若
若![]() ,则存在
,则存在![]() ,使得
,使得![]() ,从而
,从而![]() 。由于
。由于![]() ,故
,故![]() 。而
。而![]() 可知
可知![]() (
(![]() 为非零常数),这与
为非零常数),这与![]() 在
在![]() 上超越矛盾!
□
上超越矛盾!
□
 分解引理
分解引理
根据引理4,为了能够继续使用Hermite约化,我们需要将分母中的![]() 因子分离出来,这就引导我们引入如下定义。
因子分离出来,这就引导我们引入如下定义。
在这样的定义下,![]() 有广义分解
有广义分解![]() ,其中
,其中![]() 为广义多项式,
为广义多项式,![]() ,
,![]() ,
,![]() 互素,
互素,![]() 且有
且有![]() 。有类似于引理2的分解引理,证明过程也是类似的。
。有类似于引理2的分解引理,证明过程也是类似的。
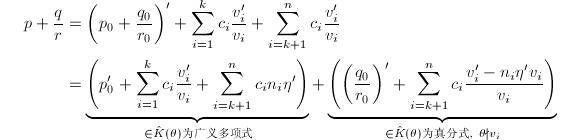
由于![]() 在
在![]() 上超越,等式两端的关于
上超越,等式两端的关于![]() 的广义多项式和真分式必定对应相等,从而
的广义多项式和真分式必定对应相等,从而
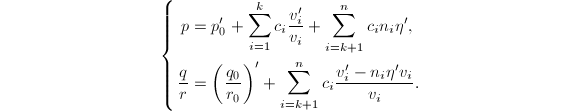 故
故
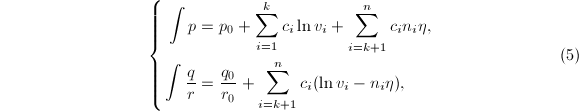 都在
都在![]() 上有初等积分。
□
上有初等积分。
□
 多项式部分
多项式部分
在式(5)中设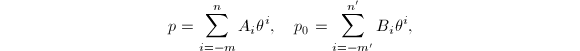 其中
其中![]() ,则有
,则有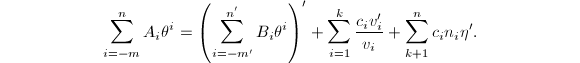 由于
由于![]() 已知,我们的目标是求出
已知,我们的目标是求出![]() 和
和![]() 。由于多项式求导不改变次数,故必有
。由于多项式求导不改变次数,故必有![]() ,
,![]() 。比较对应项系数得到
。比较对应项系数得到
![]() 这些是
这些是![]() 上的关于未知量
上的关于未知量![]() 的Risch方程,我们假定了能够在
的Risch方程,我们假定了能够在![]() 上求解此类方程或给出无解的结论。若其中有一个方程无解,则
上求解此类方程或给出无解的结论。若其中有一个方程无解,则![]() 在
在![]() 上无初等积分;否则可求出
上无初等积分;否则可求出![]() ,最后根据
,最后根据![]() 求出
求出![]() 。
。
 有理部分和对数部分
有理部分和对数部分
由于我们有了引理4的保证,依然可以对广义分解中的![]() 进行Hermite约化过程,从而得到积分的有理部分。
进行Hermite约化过程,从而得到积分的有理部分。
同样可以用类似于Rothstein-Trager的方法计算对数部分,设![]() 无平方因子,则
无平方因子,则![]() 积分的形式为
积分的形式为![]() ,可知
,可知![]() 。记
。记![]() ,则
,则![]() 及
及![]() 于是
于是
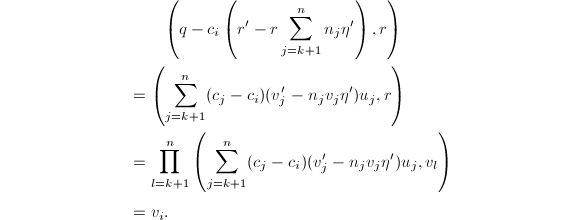 注意到
注意到![]() ,知道可以通过求结式
,知道可以通过求结式![]() 关于
关于![]() 的根来求得
的根来求得![]() 。同样的,如果此结式有根
。同样的,如果此结式有根![]() 非常数,则
非常数,则![]() 在
在![]() 上无初等积分;若所有根均为常数,则通过计算最大公因子
上无初等积分;若所有根均为常数,则通过计算最大公因子![]() 即可求得
即可求得![]() 。
。
参考文献
[1]Computer algebra: systems and algorithms for algebraic computation, Academic Press, London, UK, 1988.
[2]Symbolic Integration I: Transcendental Functions(2nd ed.), Springer Verlag, 2005.
[3]Modern Computer Algebra, Cambridge University Press, 2002.
[4]Algorithms for Computer Algebra, Kluwer Academic Publishers, 1992.
[5]The Problem of Integration in Finite Terms, Transactions of the American Mathematical Society 139 (1969), 167-189.
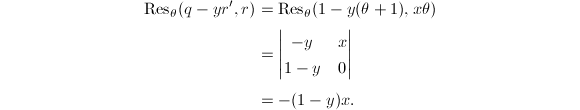 可知此结式关于
可知此结式关于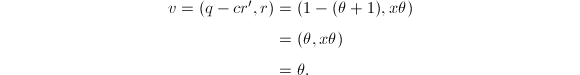 最终可知
最终可知