素数判定(the Recognition of Primes)是一个数论中十分基本,却又趣味盎然的问题.判定一个整数是否是素数,最为朴素的想法是直接利用素数的定义,用小的素数去一一试除,如果能整除的话,那就能确定无疑为合数了.统计表明,大约有76%的奇数有小于100的素因子,可见这种最平凡的方法有时十分有效.
相比整数的因子分解,素数判定一直以来被认为是较为容易的问题。2002年三位印度计算机科学家Agrawal,Kayal,Saxena[1]找到了素数判定的多项式算法(被称为AKS算法),时间复杂度为![]() 。AKS算法在理论上有重要的意义,不过实践中还要更多地考虑效率问题。实践中的素数检测方法大致分为两类,一类是确定性的,例如Lehmer
。AKS算法在理论上有重要的意义,不过实践中还要更多地考虑效率问题。实践中的素数检测方法大致分为两类,一类是确定性的,例如Lehmer ![]() 检测,Lucas
检测,Lucas ![]() 检测,椭圆曲线素性证明(ECPP)等等,当输出结果为“素数”时,能够保证被检测数一定为素数;另一类是概率性的,如Rabin-Miller检测,Baillie-PSW检测等等,当输出结果为“素数”时,仅以一定的高概率保证被检测数的素性。不过概率性检测一般要比确定性检测快得多。
检测,椭圆曲线素性证明(ECPP)等等,当输出结果为“素数”时,能够保证被检测数一定为素数;另一类是概率性的,如Rabin-Miller检测,Baillie-PSW检测等等,当输出结果为“素数”时,仅以一定的高概率保证被检测数的素性。不过概率性检测一般要比确定性检测快得多。
APRCL方法将Fermat类型的想法运用到分圆域中,最先由Adleman,Pomerance,Rumely[2]提出,后经Cohen,Lenstra[3]的改进,时间复杂度为“近似”多项式的![]() ,其中
,其中![]() 为一个常数。椭圆曲线素数证明最早由Goldwasser,Kilian[4]提出,后经Atikin,Morain[5]改进和实现,平均时间复杂度达到了
为一个常数。椭圆曲线素数证明最早由Goldwasser,Kilian[4]提出,后经Atikin,Morain[5]改进和实现,平均时间复杂度达到了![]() 。这两种方法已经成为目前实践上最快的确定性检测方法,并在密码学等领域有重要的应用。鉴于我们的目的,不能用太多篇幅来介绍这两种方法,详细可参阅文献[6].
。这两种方法已经成为目前实践上最快的确定性检测方法,并在密码学等领域有重要的应用。鉴于我们的目的,不能用太多篇幅来介绍这两种方法,详细可参阅文献[6].
有些素数判定方法严格来说应当是合性检测(Compositeness Test),这类方法总可以有效地把素数判定出来,而有可能把一个合数判定为素数.也就是说,此类方法判定一个数为合数总是准确无误的,而“漏网的”,即无法判定的合数往往称为伪素数(Pseudoprimes).
 Fermat检测
Fermat检测
几乎所有素数检测的想法之基石均为著名的Fermat小定理,即若![]() 为素数,
为素数,![]() ,则
,则![]()
由此我们得到最简单的检测算法-Fermat合性检测。
在![]() 以下,有21853个对于基
以下,有21853个对于基![]() 的Fermat伪素数[7],如果对其再进行基为
的Fermat伪素数[7],如果对其再进行基为![]() 的检测的话,伪素数将还剩下4709个,对于
的检测的话,伪素数将还剩下4709个,对于![]() 有2552个,
有2552个,![]() 有1770个.
有1770个.
运用Fermat检测的关键是如何快速计算![]() .求幂运算采取二进算法1,2,可以使用Fermat检测的算法复杂度降到平均
.求幂运算采取二进算法1,2,可以使用Fermat检测的算法复杂度降到平均![]() (其中
(其中![]() 表示乘法运算的复杂度),已经为多项式阶的算法了. 使用Montgomery约化算法3可以更进一步地提高速度。
表示乘法运算的复杂度),已经为多项式阶的算法了. 使用Montgomery约化算法3可以更进一步地提高速度。
Camichael数是看起来比Fermat伪素数条件更“苛刻”的一类数.
也就是说,Camichael数都将会是Fermat检测的“漏网之鱼”.最小的Camichael数的例子是![]() .在
.在![]() 以下一共有2163个Camichael数.(它比对基
以下一共有2163个Camichael数.(它比对基![]() 的Fermat伪素数还要来得多的原因是,如果恰巧
的Fermat伪素数还要来得多的原因是,如果恰巧![]() 有2,3,5,7的因子,
有2,3,5,7的因子,![]() 便可以是Camichael数而非Fermat伪素数)
便可以是Camichael数而非Fermat伪素数)
 Euler检测
Euler检测
Euler检测基于Euler的二次剩余定理,即若![]() 为奇素数,
为奇素数,![]() ,则
,则![]() 其中
其中![]() 是Legendre符号.
是Legendre符号.
对于Euler伪素数和强伪素数均不会出现类似Fermat伪素数的情况,也就是说,只要测试的基![]() 足够多,最终总可以将和数和素数分辩开来.
足够多,最终总可以将和数和素数分辩开来.![]() 以下只有13个同时为对基2,3,5的强伪素数.
以下只有13个同时为对基2,3,5的强伪素数.
 Lehmer
Lehmer 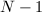 型检测
型检测
有时候![]() 的素性很难判定,而
的素性很难判定,而![]() 的分解却很容易得到.这一节的方法便是依赖于
的分解却很容易得到.这一节的方法便是依赖于![]() 的素因子分解.
的素因子分解.
寻找![]() 的生成元(甚至只寻找模
的生成元(甚至只寻找模![]() 的一个二次剩余)都是非常困难的事情,目前还没有有效的确定性的方法.一个现实的问题是如果
的一个二次剩余)都是非常困难的事情,目前还没有有效的确定性的方法.一个现实的问题是如果![]() 为伪素数,如何才能快速的找到Lehmer
为伪素数,如何才能快速的找到Lehmer ![]() 检测中符合条件的
检测中符合条件的![]() ,即
,即![]() 的一个生成元呢?有一些步骤可以采用:
的一个生成元呢?有一些步骤可以采用:
- 排除所有
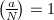 的
的 ,这就排除了一半可能的
,这就排除了一半可能的 !
! - 从较小的
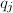 开始检测,因为
开始检测,因为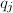 越小,失败的可能性越大.
越小,失败的可能性越大.
下面的定理让我们可以拥有不必完全分解![]() 的便利.
的便利.
 Lucas 伪素数检测与
Lucas 伪素数检测与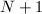 型检测
型检测
如果![]() 也是很难分解的,这里的方法就将分解的困难转移到
也是很难分解的,这里的方法就将分解的困难转移到![]() 上去.想法是与
上去.想法是与![]() 型检测是类似的, 不过要将Fermat小定理从
型检测是类似的, 不过要将Fermat小定理从![]() 上到二次域的代数整数环上去,替代那里的
上到二次域的代数整数环上去,替代那里的![]() 的则是所谓Lucas序列
的则是所谓Lucas序列![]() .
.
设![]() 为无平方整数,记
为无平方整数,记![]() 为二次域
为二次域![]() 的代数整数环,我们熟知(参见[9],P139)当
的代数整数环,我们熟知(参见[9],P139)当![]() 时,
时,![]() 而当
而当![]() 时,
时,![]()
在![]() 中可以很容易地讨论同余的概念,称
中可以很容易地讨论同余的概念,称![]() ,若
,若![]() 属于
属于![]() 在
在![]() 中生成的理想。记
中生成的理想。记![]() 为
为![]() 在
在![]() 中的共轭,即
中的共轭,即![]() ,则在
,则在![]() 中我们有如下Fermat小定理的类比。
中我们有如下Fermat小定理的类比。
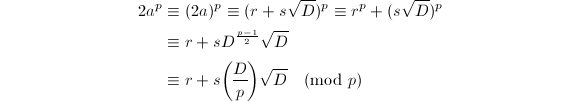 从而得到所要结论。
□
从而得到所要结论。
□
定理6中的乘幂不容易计算,为了有效地利用定理6的结论,我们引入Lucas序列的概念,Lucas序列实际上是一类简单的二阶递推序列。
由于![]() 模
模![]() 可逆,
可逆,![]() ,从而
,从而![]() 引理得证。
□
引理得证。
□
由上面的定理我们自然地得到Lucas伪素数的概念。
正如我们在Fermat检测和Euler检测中看到的,一个伪素数概念对应着一个合性检测算法,由此我们立即可以到得到Lucas伪素数检测算法。
我们已经得到了Lucas伪素数合性检测,和![]() 型检测类似,我们还能够进行素性的确证。在这里,替代
型检测类似,我们还能够进行素性的确证。在这里,替代![]() 的分解的是
的分解的是![]() 的分解,我们可以看到下面的定理与定理1是多么的“形似”。
的分解,我们可以看到下面的定理与定理1是多么的“形似”。
与![]() 型检测完全类似还可以得到以下结果.
型检测完全类似还可以得到以下结果.
 概率性的检测方法
概率性的检测方法
更加富有趣味的是素性的概率性检测方法,Knuth这样评价道概率性的算法[12]:“与其说算法重复地猜测错,倒不如说由于硬件的失灵或宇宙射线的原因,我们的计算机在它的计算中丢了一位.”概率性的算法使我们对传统的可靠性产生疑问:我们是否真的需要“素性”的严格确证?概率性算法最早由Solovay,Strassen[13]于1974年提出,Rabin-Miller的改进方法为Mathematica软件所采用. Baillie-PSW检测则综合了各种概率性检测方法,目前为止仍没有找到失败的反例,并且已经验证检测对于![]() 以下的整数均是正确的。
以下的整数均是正确的。
 Solovay-Strassen检测
Solovay-Strassen检测
如果![]() 能分解为两个互素的非平凡因子
能分解为两个互素的非平凡因子![]() ,
,![]() ,我们证明必有
,我们证明必有![]() 满足
满足![]() 都有
都有![]() (由Jacobi符号的性质便知这是不可能的).若不然,由中国剩余定理找到
(由Jacobi符号的性质便知这是不可能的).若不然,由中国剩余定理找到![]() 满足
满足![]() 且
且![]() .则有
.则有![]() 且
且![]() ,而这与
,而这与![]() 是矛盾的!
是矛盾的!
如果![]() 为素数幂,则
为素数幂,则![]() 满足
满足![]() 都有
都有![]() ,再由Euler定理知道
,再由Euler定理知道![]() .而这也是不可能的.
□
.而这也是不可能的.
□
 Rabin-Miller检测
Rabin-Miller检测
Solovay-Strassen检测利用了Euler伪素数“并不多”的性质,使用随机给出的基![]() 多次重复进而给出高成功率的素性检测结果。同样的想法也可以施用于强伪素数与Lucas伪素数,后者便是著名的Rabin-Miller检测,后者则被运用到Baillie-PSW检测中。
多次重复进而给出高成功率的素性检测结果。同样的想法也可以施用于强伪素数与Lucas伪素数,后者便是著名的Rabin-Miller检测,后者则被运用到Baillie-PSW检测中。
Rabin-Miller检测可以看成我们在注1中的想法的一个具体化.
 Baillie-PSW检测
Baillie-PSW检测
只是使用多基的Rabin-Miller测试可能得不到好的效率。Baillie[15]将基为2的Rabin-Miller检测与Lucas伪素数检测结合起来,得到更为有效的素数检测方法。Pomerance, Selfridge, Wagstaff在[7]中对![]() 的数进行了验证算法的正确性。尽管Pomerance[16]指出对于充分大的
的数进行了验证算法的正确性。尽管Pomerance[16]指出对于充分大的![]() ,必定有Baillie-PSW检测的反例,并且以30美元悬赏找出一个算法失败的反例(后来增加到620美元),不过反例至今没有找到,并且有经验估计认为第一个反例如果被找到的话,至少得有10000个十进位长度[17]。
,必定有Baillie-PSW检测的反例,并且以30美元悬赏找出一个算法失败的反例(后来增加到620美元),不过反例至今没有找到,并且有经验估计认为第一个反例如果被找到的话,至少得有10000个十进位长度[17]。
下面我们正式给出Baillie-PSW检测。
参考文献
[1]PRIMES is in P, Annals of Mathematics 160 (2004), no.2, 781 – 793.
[2]On Distinguishing Prime Numbers from Composite Numbers, The Annals of Mathematics 117 (1983), no.1, 173--206.
[3]Primality Testing and Jacobi Sums, Mathematics of Computation 42 (1984), no.165, 297--330.
[4]Almost all primes can be quickly certified, Proceedings of the eighteenth annual ACM symposium on Theory of computing, 1986, 316 - 329.
[5]Elliptic curves and primality proving, Mathematics of Computation 61 (1993), 29 - 68.
[6]A Course in Computational Algebraic Number Theory, Springer Verlag, 1993.
[7]The Pseudoprimes to $25 \cdot 10^9$, Mathematics of Computation 35 (1980), no.151, 1003--1026.
[8]Fermat numbers and Mersenne numbers, Mathematics of Computation 18 (1964), 146-148.
[9]代数学引论, 高等教育出版社, 北京, 2000.
[10]An Extended Theory of Lucas' Functions, The Annals of Mathematics 31 (1930), no.3, 419--448.
[11]A Really Trivial Proof of the Lucas-Lehmer Test, The American Mathematical Monthly 100 (1993), no.4, 370--371.
[12]The art of computer programming, volume 2 (3rd ed.): seminumerical algorithms, Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA, 1997.
[13]A Fast Monte-Carlo Test for Primality, SIAM Journal on Computing 6 (1977), no.1, 84-85.
[14]Probabilistic algorithm for testing primality, Journal of Number Theory 12 (1980), no.1, 128-138.
[15]Lucas Pseudoprimes, Mathematics of Computation 35 (1980), no.152, 1391 - 1417.
[16]Are There Counterexamples to the Baillie-PSW Primality Test?, 1984, http://www.pseudoprime.com/dopo.pdf.
[17]Re: Baillie-PSW - Which variant is correct?, 2004, http://groups.google.com/group/sci.crypt/msg/48ec324b9fc9f866.
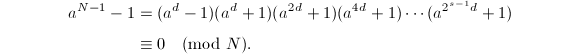
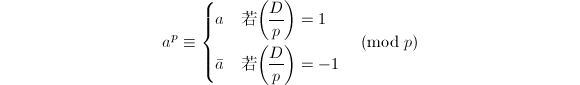
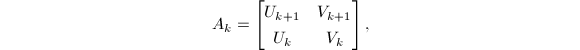 则有
则有
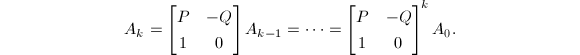 可以使用快速求幂的方法在
可以使用快速求幂的方法在