设![]() 为UFD(即唯一析因整环,例如
为UFD(即唯一析因整环,例如![]() ),
),![]() 为域(例如
为域(例如![]() ),则
),则![]() 也是UFD,对其上两多项式可讨论GCD问题.最古典的方法即是Euclid算法。然而,在上世纪六十年代末一些试验中发现这种算法在
也是UFD,对其上两多项式可讨论GCD问题.最古典的方法即是Euclid算法。然而,在上世纪六十年代末一些试验中发现这种算法在![]() 或
或![]() 中的系数增长很快,甚至于指数式。
中的系数增长很快,甚至于指数式。
为了解决这一问题,1971年,Collins,Brown提出了UFD上的多项式模最大公因子算法。对于多元情形,Mozes和Yun于1973年提出了基于Hensel提升方法的模因子算法。下面对经典的Euclid算法和改进算法进行论述。
 Euclid算法
Euclid算法
在Euclid整环![]() 中,我们有如下的Euclid除法:
中,我们有如下的Euclid除法:
![]() 是Euclid整环,因而有以下的扩展Euclid算法:
是Euclid整环,因而有以下的扩展Euclid算法:
实际上在计算机中进行的是![]() 上的运算,我们总可以找到整数乘到该多项式上使其化为
上的运算,我们总可以找到整数乘到该多项式上使其化为![]() 上的多项式。
上的多项式。
类似的结论还有以下一些命题,相关内容可参阅相关的高等代数学内容,如[1].
于是有下面的:
尽管![]() 不是Euclid整环,但我们可引入
不是Euclid整环,但我们可引入![]() 上的伪除法,来构造类似Euclid余式序列。
上的伪除法,来构造类似Euclid余式序列。
在用伪除法求最大公因子时就会导致系数增长很快,在后面介绍素数模方法之前,我们可以用下面定义的几个多项式余式序列一定程度上减小系数增长速度。
 域上多项式的快速Euclid算法
域上多项式的快速Euclid算法
1938年Lehmer最先提出了快速Euclid算法,后来Knuth(1970),Schoenhage(1971),Moenck(1973),Aho,Hopcroft,UUman(1978),Schwartz(1980),Brent,Gustavson,Yun(1980),Strassen(1983)对这些算法也有论述。
在域(例如![]() )中,Euclid算法可表示为(各
)中,Euclid算法可表示为(各![]() 均为首一的):
均为首一的):
![]()
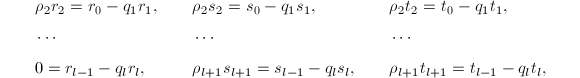
若设![]() ,还可记
,还可记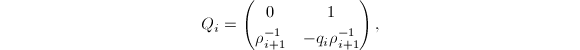 则
则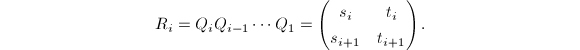
易知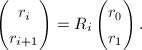
在随机情况下,可证明域![]() 中
中![]() 的概率
的概率![]() ,当素数
,当素数![]() 很大时,可认为
很大时,可认为![]() 序列的下降速度很慢。为了说明快速Euclid算法,我们先引入下面一些定义和定理。该算法的基本原理在于利用多项式的前某些系数来计算余式序列.
序列的下降速度很慢。为了说明快速Euclid算法,我们先引入下面一些定义和定理。该算法的基本原理在于利用多项式的前某些系数来计算余式序列.
易知该等价关系有如下性质:
关于![]() -度重合,有如下重要的命题:
-度重合,有如下重要的命题:
(1)首先我们有如下四个不等式:
![]() ,
,
![]() (注意
(注意![]() -截式取多项式的前
-截式取多项式的前![]() 项),
项),
![]() ,
,
![]() ,
,
根据上面的不等式,由![]() 可知
可知![]() ,故
,故![]() .
.
(2)假定![]() 且
且![]() ,则首先显然有
,则首先显然有![]()
另外,
![\begin{align*}
\mathrm{deg}(r-r^*)&\le\max\{\mathrm{deg}(f-f^*),\mathrm{deg}q+\mathrm{deg}(g-g^*)\}\notag\\
&<\mathrm{deg}q+\mathrm{deg}f-2k\notag\\
&=\mathrm{deg}g-2(k-\mathrm{deg}q)\notag\\
&=\mathrm{deg}r-[2(k-\mathrm{deg}q)-(\mathrm{deg}g-\mathrm{deg}r)],\notag
\end{align*}](./latex/latex2png-PolyGCD_254469762_.gif)
又由假设有![]() ,
,
于是![]() ,
,
故![]() .
□
.
□
下面考虑两个首一的多项式Euclid余式序列:

分别令![]() ,对
,对![]() ,定义
,定义![]() ,且显然有
,且显然有![]()
下面的定理是快速Euclid算法的基础:
由此我们可以得到下面的算法:
输入:首一多项式![]() ,其中
,其中![]() ,
,
输出:![]() 以及
以及![]() .
.
- 如果
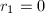 或
或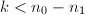 ,则输出
,则输出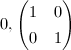 ,
, 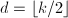 ,
,- 递归调用本算法,输入
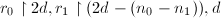 ,并将结果输出至
,并将结果输出至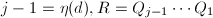 ,
, - 赋值
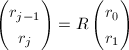 ,
,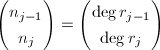 ,
, - 如果
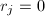 或者
或者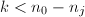 则输出
则输出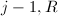 ,
, - 赋值
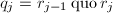 ,
,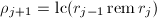 ,
,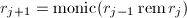 ,
,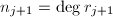 ,
,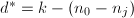 ,
, - 递归调用本算法,输入
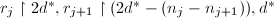 ,并将结果输出至
,并将结果输出至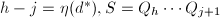 ,
, - 赋值
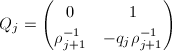 ,
, - 输出
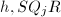 .
.
后面将会提到![]() 上的素数模公因子算法,而
上的素数模公因子算法,而![]() 为一域,如果再用到本节所提到的快速Euclid算法,则可提高计算效率。
为一域,如果再用到本节所提到的快速Euclid算法,则可提高计算效率。
 结式与子结式
结式与子结式
 结式
结式
对于多项式最大公因子问题,结式理论纯粹是一个概念上的工具,并没有用于算法中,但是对于它们的分析对后面的GCD算法理论有重要的作用(见[2]P142).然而结式的计算在某些问题中却十分重要,如符号积分中将要计算的Rothstein-Trager结式(可参见后文有关章节).因此前两小节介绍结式和子结式,第三小节讲它们的计算方法.
令![]() ,若
,若![]() ,则
,则![]() ,令
,令![]() ,
,![]() 则满足。
则满足。
反过来,设存在这样的![]() ,
,![]() ,若
,若![]() ,
,![]() 互素,则
互素,则![]() ,这与
,这与![]() 且
且![]() 矛盾,因此
矛盾,因此![]() .
□
.
□
如果记![]() ,其中
,其中![]() ,
,![]() ,则线性映射
,则线性映射![]() 可在自然基
可在自然基![]() 下表示矩阵是Sylvester矩阵:
下表示矩阵是Sylvester矩阵:
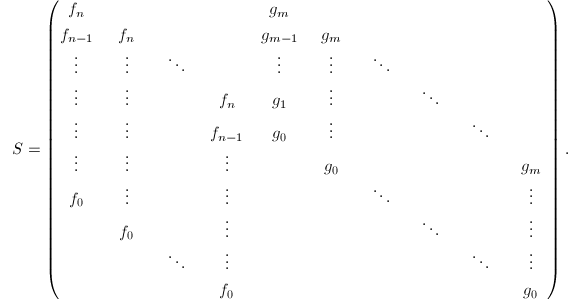
上面的定理用矩阵语言描述即为:
对于一些特殊情况,当![]() 时
时![]() 是空矩阵,且结式为1。若
是空矩阵,且结式为1。若![]() 为0或非常数多项式,则
为0或非常数多项式,则![]() ,若
,若![]() 是非零常数则
是非零常数则![]() .前面定理在这些情形下仍然成立.
.前面定理在这些情形下仍然成立.
再假设![]() ,令
,令![]() 为最小的指标使得
为最小的指标使得![]() ,此时将Sylvester矩阵分块,去掉左
,此时将Sylvester矩阵分块,去掉左![]() 列和上
列和上![]() 行,只留下右下
行,只留下右下![]() 的方阵
的方阵![]() ,显然
,显然![]() ,于是
,于是![]() ,于是引理得证。
□
,于是引理得证。
□
 子结式
子结式
设![]() 为任一域,
为任一域,![]() ,
,![]() 是
是![]() 上非零多项式,其
上非零多项式,其![]() 的次数
的次数![]() 大于等于
大于等于![]() 的次数
的次数![]() .如同快速Euclid算法一节所列表格,我们再次将Euclid算法的过程表示如下(各
.如同快速Euclid算法一节所列表格,我们再次将Euclid算法的过程表示如下(各![]() 均为首一的):
均为首一的):
![]()
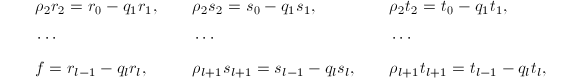
对此有如下的
为了将上面的内容翻译成一种代数语言,我们考虑上一节定义的线性映射![]() 在
在![]() 上的限制.然而我们容易知道,该映射的象是在空间
上的限制.然而我们容易知道,该映射的象是在空间![]() 中,为了使得其具有在满足某些条件下有成为同构的可能性,我们要使两个空间维数相等.进而我们考虑了如下的线性映射:
中,为了使得其具有在满足某些条件下有成为同构的可能性,我们要使两个空间维数相等.进而我们考虑了如下的线性映射:![]() ,其满足
,其满足![]()
我们有如下的推论:
我们记![]() 的矩阵形式为
的矩阵形式为![]() ,其也取为自然基上的表示,为Sylvester矩阵的子矩阵:
,其也取为自然基上的表示,为Sylvester矩阵的子矩阵:

 Euclid算法计算子结式
Euclid算法计算子结式
我们一步步来推出子结式的计算方法.首先我们有如下引理:
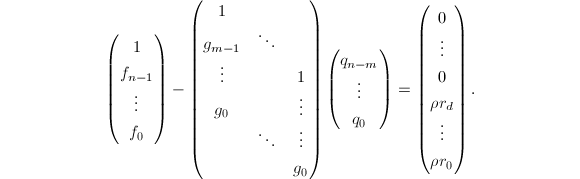 由此可以对
由此可以对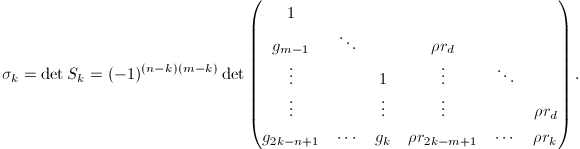 上面的矩阵用分块可表示为如下形式:
上面的矩阵用分块可表示为如下形式:
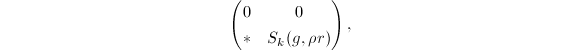 因此,
因此,进而我们有下面的定理:
对于(2),只需化简![]() ,有
,有
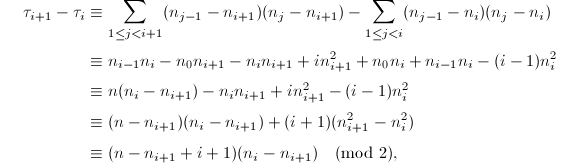 于是显然可以得到(2)中的递推式.
□
于是显然可以得到(2)中的递推式.
□
取![]() ,则
,则![]() 即为结式,因此我们得到如下计算结式的方法:
即为结式,因此我们得到如下计算结式的方法:
事实上,对于![]() 是UFD的情况,上面推论一般也是成立的.例如下面举了一个
是UFD的情况,上面推论一般也是成立的.例如下面举了一个![]() 的例子来说明:
的例子来说明:

![$\mathbb{Z}[x]$](./latex/latex2png-PolyGCD_27044286_-5.gif) 中的模GCD算法
中的模GCD算法
模算法基于的思想是将整数环中的运算化为有限域上的运算,最后通过中国剩余定理算法将有限域中结果还原到整数环中.例如有两个多项式![]() ,考虑素数
,考虑素数![]() ,令
,令![]() ,我们要求
,我们要求![]() ,那么就可以用有限域中的结果
,那么就可以用有限域中的结果![]() 来代替
来代替![]() ,然而若要
,然而若要![]() ,我们需要Mignotte界的保证.对于
,我们需要Mignotte界的保证.对于![]() ,其成立的条件我们后面也会给出理论上的分析.
,其成立的条件我们后面也会给出理论上的分析.
 Mignotte界
Mignotte界
由线性赋范空间的相关内容易如有如下结论:![]()
首先我们有如下的引理:
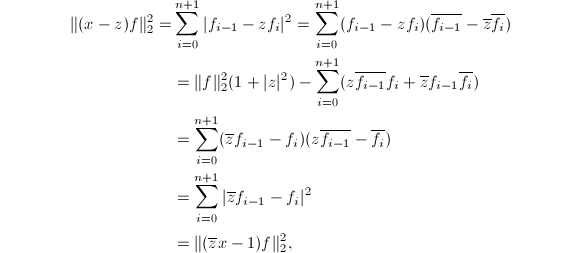 证毕.
□
证毕.
□
此由三角函数系的正交归一性显然可以看出.于是
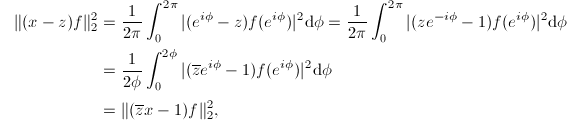 证毕.
□
证毕.
□
若![]() 是
是![]() 的
的![]() 个复根,则显然有
个复根,则显然有![]() .
.
显然,![]() 且
且![]() .
.
关于上面定义的![]() ,还有下面的:
,还有下面的:
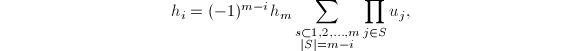 于是
于是
 大素数模公因子算法(Big Prime Modular Gcd Algorithm)
大素数模公因子算法(Big Prime Modular Gcd Algorithm)
如不作特殊说明,本小节中![]() 域取代表元
域取代表元![]() .若记
.若记![]() 的首项系数为
的首项系数为![]() ,则定义其首一多项式为
,则定义其首一多项式为![]()
设![]() ,且
,且![]() ,则
,则![]() 是一非零常数,且满足
是一非零常数,且满足![]() .此由Hadamard不等式
.此由Hadamard不等式
![]() 可知,见[2].
可知,见[2].
下面的定理保证了算法4中判定条件的正确性.
事实上,我们对算法4中的条件稍加改变,仍然可行:
于是,![]() ,因而
,因而![]() .
□
.
□
算法中是随机从区间![]() 中选取一个素数,这种随机性是否保证我们能较快地得到正确的结果呢?下面的定理作出了回答。
中选取一个素数,这种随机性是否保证我们能较快地得到正确的结果呢?下面的定理作出了回答。
只需证若![]() 不同时整除
不同时整除![]() ,
,![]() ,且
,且![]() ,则
,则![]() .
.
首先![]() ,若
,若![]() ,则由首一性知
,则由首一性知![]() ,否则
,否则![]() ,此时由
,此时由![]() 可得
可得![]() .而存在
.而存在![]() 使
使
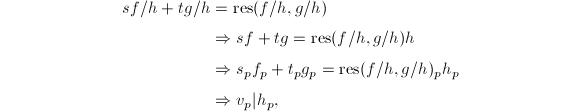 故仍有
故仍有![]() .
□
.
□
 小素数模公因子算法(Small Prime Modular Gcd Algorithm)
小素数模公因子算法(Small Prime Modular Gcd Algorithm)
下面仅给出小素数模方法的两种实现。其中算法6参考[2],算法7参考[3],两者的思想基本上是一样的.其中在两个算法中任取素数时都加上了限制![]() ,此参看[2]生成素数的有关章节.从算法的实现细节上来说,第二个算法比第一个算法略优,其能减少很多不必要的计算.
,此参看[2]生成素数的有关章节.从算法的实现细节上来说,第二个算法比第一个算法略优,其能减少很多不必要的计算.
输入:![]() 上本原多项式
上本原多项式![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
输出:![]() .
.
- 赋值
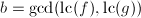 ,
,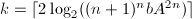 ,
,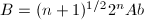 ,
,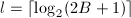 ,
, - 任取含
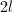 个不同的素数的集合
个不同的素数的集合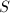 ,且
,且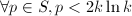 ,
, 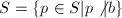 ,
,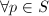 ,
,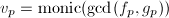 ,
,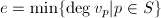 ,
,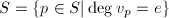 ,
,- 若
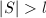 则去掉
则去掉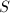 中
中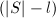 个元素,只保留
个元素,只保留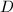 个,否则转到第2步,
个,否则转到第2步, - 用中国剩余定理计算
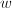 ,
,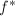 ,
,![$g^*\in\mathbb{Z}[x]$](./latex/latex2png-PolyGCD_57891172_-5.gif) 使得
使得
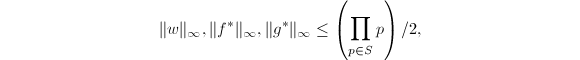 且
且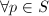 有
有
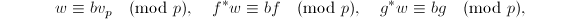
- 若
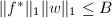 且
且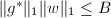 则继续下一步,否则转到第2步,
则继续下一步,否则转到第2步, - 输出
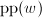 .
.
输出:![]() .
.
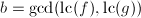 ,
,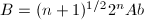 ,
,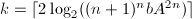 ,
,- 任取素数
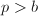 (实际上
(实际上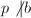 即可),且
即可),且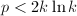 ,
, ![$v_p=\gcd(f_p,g_p)\in\mathbb{Z}_p[x]$](./latex/latex2png-PolyGCD_205216551_-5.gif) ,
,- 若
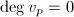 则输出1,
则输出1, 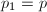 ,
,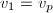 ,
,- 若
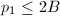 ,则执行下一步,否则跳转第12步,
,则执行下一步,否则跳转第12步, - 再取素数
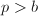 (or
(or 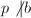 ),且
),且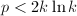 ,
,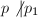 ,令
,令![$v_p=\gcd(f_p,g_p)\in\mathbb{Z}_p[x]$](./latex/latex2png-PolyGCD_205216551_-5.gif) ,
, - 若
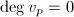 则输出1,
则输出1, - 若
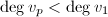 ,则
,则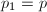 ,
,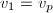 ,并跳至第6步,
,并跳至第6步, - 若
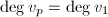 则由中国剩余定理计算
则由中国剩余定理计算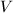 使得
使得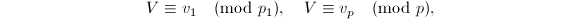 并赋值
并赋值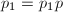 ,
,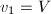 ,
, - 转回第6步,
- 若
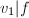 且
且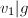 则继续,否则转回第2步,
则继续,否则转回第2步, - 输出
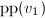 .
.
 多项式组的概率算法
多项式组的概率算法
下面引进在一元多项式GCD算法中又一个概率性的算法。对于多项式组来说,我们当然可以一步一步求每两个多项式的最大公因子得到整个多项式组的最大公因子,然而用下面的概率算法虽然得到的是可能解,效率却更高。
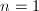 情形显然。将
情形显然。将 写成
写成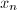 的多项式
的多项式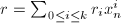 ,其中
,其中![$r_i\in R[x_1,\ldots,x_{n-1}]$](./latex/latex2png-PolyGCD_249212532_-5.gif) 且
且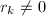 ,由于
,由于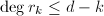 ,则由归纳假设,
,则由归纳假设,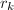 在
在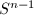 中至多有
中至多有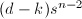 个零点,于是
个零点,于是 和
和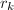 至多在
至多在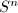 中有
中有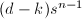 个零点。并且
个零点。并且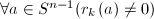 ,
,![$r_a=\sum_{0\le i\le k}r_i(a)x_n^i\in R[x_n]$](./latex/latex2png-PolyGCD_208445081_-9.gif) 至多有
至多有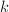 个零点,因此零点数目上限可估为:
个零点,因此零点数目上限可估为: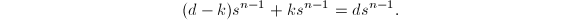
- 由1显然得到.
□
若从![]() 中随机选取
中随机选取![]() ,则有
,则有![]() .下面假设我们有一个有限集
.下面假设我们有一个有限集![]() 和一个
和一个![]() 上随机数发生器,则有下面的:
上随机数发生器,则有下面的:
用快速Euclid算法替换其中计算,还可提高效率。
实际过程中,可以取![]() 为最小次数的多项式,以使错误概率降低,并且在算法结束后检验
为最小次数的多项式,以使错误概率降低,并且在算法结束后检验![]() 是否为所求的最大公因子,若不是,则重新选取随机数计算,直至输出正确结果。
是否为所求的最大公因子,若不是,则重新选取随机数计算,直至输出正确结果。
参考文献
[1]代数学引论, 高等教育出版社, 北京, 2000.
[2]Modern Computer Algebra, Cambridge University Press, 2002.
[3]计算机代数基础---代数与符号计算的基本原理, 科学出版社, 2005.
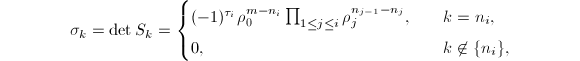 其中
其中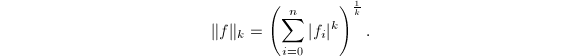
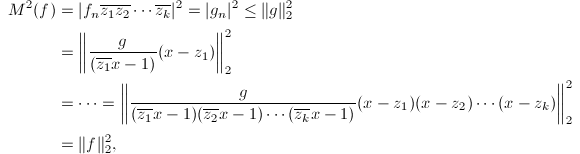 证毕.
证毕.