 Risch 微分方程
Risch 微分方程
在考虑超越指数函数积分时我们遇到了形如![]() 的微分方程(6),其中数
的微分方程(6),其中数![]() (基域)为已知函数,
(基域)为已知函数,![]() 为未知函数。这是一个Risch微分方程的求解问题。一般地,设
为未知函数。这是一个Risch微分方程的求解问题。一般地,设![]() ,Risch微分方程问题就是要判断
,Risch微分方程问题就是要判断
![]() 在
在![]() 中是否有解,如果有解则构造出解。此问题是最简单的一类微分方程,同时对于符号积分的求解过程也是本质上重要的。
中是否有解,如果有解则构造出解。此问题是最简单的一类微分方程,同时对于符号积分的求解过程也是本质上重要的。
 有理函数域
有理函数域
首先我们假定最简单的有理函数域情形,即设![]() 、
、![]() 或
或![]() 。记
。记![]() 表示有理函数
表示有理函数![]() 的既约分母,对于任意
的既约分母,对于任意![]() 为不可约多项式且
为不可约多项式且![]() ,我们希望求出
,我们希望求出![]() 的次数。设
的次数。设![]() ,
,![]() ,
,![]() 。可令
。可令![]() ,其中
,其中![]() ,则
,则![]() ,由
,由![]() 可知
可知![]() 。故方程(1)中三项
。故方程(1)中三项![]() ,
,![]() ,
,![]() 的分母中
的分母中![]() 的次数分别为
的次数分别为![]() ,
,![]() ,
,![]() 。比较两端分母中
。比较两端分母中![]() 的次数,分为三种情形:
的次数,分为三种情形:
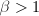 时,必有
时,必有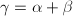 ;
;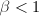 时,必有
时,必有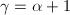 ;
;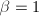 时,
时,
- 若左端求和后无约分,则
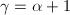 ;
; - 若左端求和后有约分。由
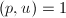 可找到
可找到 ,
,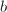 ,使得
,使得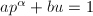 ,从而
,从而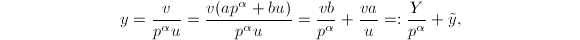 满足
满足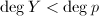 ,
,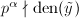 。同理可设
。同理可设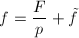 满足
满足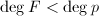 ,
,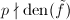 。从而
。从而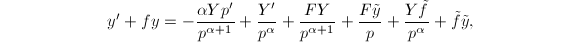 由于有约分,左端求和分母为
由于有约分,左端求和分母为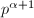 的项必定消去,可知
的项必定消去,可知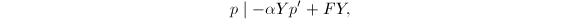 而
而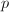 不可约,
不可约,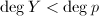 ,故
,故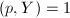 ,可得
,可得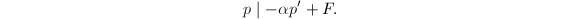 又由
又由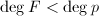 可知必有
可知必有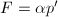 ,即
,即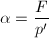 。
。
- 若左端求和后无约分,则
由此得到了未知函数![]() 分母中
分母中![]() 的次数
的次数![]() 的上界,使我们便于使用待定系数法。
的上界,使我们便于使用待定系数法。
仔细验证可以发现,只有在论证![]() 时用到了
时用到了![]() 为不可约多项式,其他地方均可以将条件减弱为
为不可约多项式,其他地方均可以将条件减弱为![]() 为无平方因子的多项式。因此可以首先用
为无平方因子的多项式。因此可以首先用![]() 的无平方因子分解代替完全分解。需要处理的是对幂次
的无平方因子分解代替完全分解。需要处理的是对幂次![]() 的无平方因子
的无平方因子![]() ,求出
,求出![]() 的不可约因子
的不可约因子![]() ,使得
,使得![]() 为整数。与Rothstein-Trager方法类似得论证可以得到
为整数。与Rothstein-Trager方法类似得论证可以得到![]() 从而我们只需求结式
从而我们只需求结式![]() 关于
关于![]() 的整数根即可。我们得到了如下计算
的整数根即可。我们得到了如下计算![]() 的一个倍数的方法。
的一个倍数的方法。
在得到![]() 的一个倍数之后,只要确定
的一个倍数之后,只要确定![]() 分母次数的一个上界,即可使用待定系数法求出
分母次数的一个上界,即可使用待定系数法求出![]() 的分母来了。设
的分母来了。设![]() ,我们希望求出记
,我们希望求出记![]() 。带入方程(1)并两端乘以最小公分母可以得到形如
。带入方程(1)并两端乘以最小公分母可以得到形如![]() 的等式,其中
的等式,其中![]() 为多项式,记
为多项式,记![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 的次数分别为
的次数分别为![]() ,
,![]() ,
,![]() 。比较等式两端的次数,分为三种情形:
。比较等式两端的次数,分为三种情形:
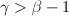 时,必有
时,必有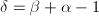 ;
;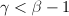 时,必有
时,必有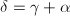 ;
;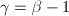 时,
时,
- 若左端求和后最高项未被消去,则
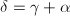 ;
; - 若左端求和后最高项被消去。设
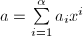 ,
,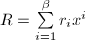 ,
,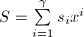 ,则有
,则有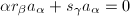 ,从而
,从而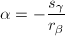 。
。
- 若左端求和后最高项未被消去,则
由此我们得到了![]() 分母次数
分母次数![]() 的一个上界。
的一个上界。
有了引理2,接下来便可以对![]() 的分母进行待定系数法求解了,最终可得到方程(1)在
的分母进行待定系数法求解了,最终可得到方程(1)在![]() 、
、![]() 或
或![]() 的解
的解![]() 。
。
 一般情形
一般情形
上面我们讨论了![]() 为最简单的有理函数域的情形。对于一般情形,Bronstein[3]证明了如下定理。
为最简单的有理函数域的情形。对于一般情形,Bronstein[3]证明了如下定理。
由于Risch[2], Rothstein[4], Davenport[5]解决了超越初等扩张的积分问题和Risch方程问题,Trager[6],Davenport[7]解决了代数扩张的积分问题和Risch方程问题。从而根据定理1,便可以从理论上得到所有初等函数的初等积分和Risch方程问题的解决方案了。
 一阶线性微分方程
一阶线性微分方程
求积分实际上就是最简单的一阶方程![]() ,不过可以看到解决此问题的难度已经相当大了。Risch微分方程是最简单的一类一阶微分方程(线性方程),当然我们求的仅仅是
,不过可以看到解决此问题的难度已经相当大了。Risch微分方程是最简单的一类一阶微分方程(线性方程),当然我们求的仅仅是![]() 中的解,而非
中的解,而非![]() 上的初等函数解。我们知道一阶线性方程(1)有通解表达式
上的初等函数解。我们知道一阶线性方程(1)有通解表达式![]() 但这并没有解决一般问题,因为为了算出表达式中的指数积分,我们还得回到解Risch方程问题上。
但这并没有解决一般问题,因为为了算出表达式中的指数积分,我们还得回到解Risch方程问题上。
不过以下的定理[1]使我们能够避免循环论证而得到![]() 上可能的初等函数解。
上可能的初等函数解。
- 若
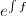 在
在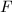 上代数,则由Liouville定理,
上代数,则由Liouville定理,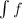 必为
必为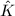 上对数函数的和,从而
上对数函数的和,从而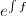 必也在
必也在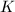 上代数。
上代数。 - 若
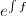 在
在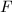 上超越,由于
上超越,由于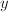 在
在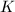 上初等,自然在
上初等,自然在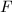 上初等,故
上初等,故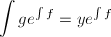 也在
也在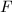 上初等。记
上初等。记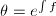 为
为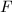 上的超越指数函数,由分解引理可知
上的超越指数函数,由分解引理可知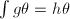 ,其中
,其中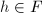 (注意指数函数求导后次数不变),从而有解
(注意指数函数求导后次数不变),从而有解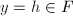 。若
。若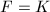 ,则有
,则有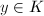 ,否则
,否则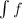 中必有
中必有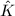 上的对数函数。可设
上的对数函数。可设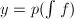 ,其中
,其中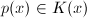 ,而由方程(1)可得
,而由方程(1)可得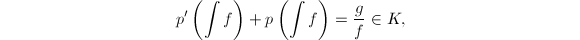 可知必有
可知必有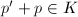 ,也有
,也有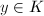 。
。
这就完成了证明。 □
因此求一阶线性方程可以通过求![]() 中的解,或是
中的解,或是![]() 上的代数函数积分来完成。
上的代数函数积分来完成。
 微分Galois理论
微分Galois理论
接下来要讨论的自然是一般高阶线性方程如何求解的问题。对一般的高阶线性方程![]() 可化为线性方程组矩阵形式
可化为线性方程组矩阵形式![]() 其中
其中
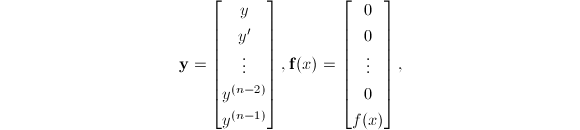
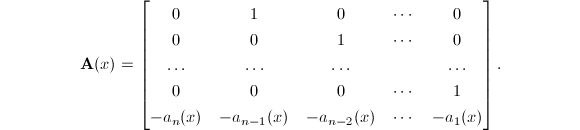
设对应的齐次方程的基本解矩阵为![]() ,则非齐次线性方程的通解为[8]
,则非齐次线性方程的通解为[8]![]() 因此我们可以首先考虑齐次方程的求解。
因此我们可以首先考虑齐次方程的求解。
在求解多项式方程的过程中诞生了伟大的Galios理论,解线性微分方程也有一个对应物——微分Galois理论。在这里我们做一个简要介绍,这些理论也是Kovacic著名的二阶线性方程求解算法的基础(尽管最终的算法可以完全摆脱微分Galois理论的语言)。首先引入几个重要的概念[9]。
下面的将微分Galois群与代数群建立联系的基本结果是本质上重要的。
定理的证明需要较多的准备,因此我们在这里只给出几个例子。
 Lie-Kolchin定理
Lie-Kolchin定理
我们可以考虑比初等函数更广的一类函数,应用起来也更加方便。
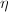 在
在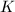 上是代数的,即有
上是代数的,即有![$f(x)\in K[x]$](./latex/latex2png-DifferentialEquation_40994369_-5.gif) 使得
使得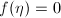 ;
;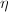 在
在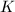 上是原函数,即有
上是原函数,即有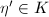 ;
;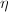 在
在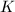 上是原函数的指数,即有
上是原函数的指数,即有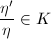 。
。
称![]() 为
为![]() 上的一个Liouville函数域,若
上的一个Liouville函数域,若![]() ,
,![]() 为
为![]() 上的Liouville生成元。
上的Liouville生成元。![]() 上的任一个Liouville函数域中的元素称为
上的任一个Liouville函数域中的元素称为![]() 上的Liouville函数。
上的Liouville函数。
线性微分方程的优美理论将引导我们,把方程Liouville解与一般线性群![]() 的代数子群联系到一起。下面理论上重要的Lie-Kolchin定理给出了线性微分方程的解是Liouville解的充要条件。
的代数子群联系到一起。下面理论上重要的Lie-Kolchin定理给出了线性微分方程的解是Liouville解的充要条件。
因此为了研究线性微分方程的Liouville解,我们可以转向代数子群的研究。比如说对于二阶线性方程,我们便需要对特殊线性群![]() 的代数子群有所了解。
的代数子群有所了解。
 二阶线性微分方程
二阶线性微分方程
考虑二次齐次线性方程![]() 其中
其中![]() ,通过标准的变换
,通过标准的变换![]() (
(![]() 中的积分总可以求出),可化为缺项形式
中的积分总可以求出),可化为缺项形式![]() 因此我们下面可以只考虑形如
因此我们下面可以只考虑形如
![]() 其中
其中![]() 的二阶线性方程。在这样的特殊形式下我们知道,若
的二阶线性方程。在这样的特殊形式下我们知道,若![]() 是一个Liouville解的话,那么
是一个Liouville解的话,那么![]() 是与
是与![]() 线性无关的另一个解[8],从而方程所有的解都是
线性无关的另一个解[8],从而方程所有的解都是![]() 上的Liouville解。
上的Liouville解。
正如上面所说的,特殊线性群![]() 的代数子群对于我们很重要,事实上有下面的定理(见[10])。
的代数子群对于我们很重要,事实上有下面的定理(见[10])。
对应于代数子群的四个类型,如下定理就不令人意外了。
- 有一个解
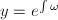 为Liouville解,其中
为Liouville解,其中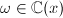 ;
; - 有一个解
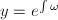 为Liouville解,其中
为Liouville解,其中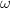 为
为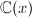 上的二次代数元,且第一类情形不成立;
上的二次代数元,且第一类情形不成立; - 所有解
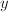 在
在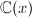 上是代数的,为Liouville解,且前两类情形不成立;
上是代数的,为Liouville解,且前两类情形不成立; - 无Liouville解。
- 可假设
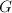 是上三角的,由
是上三角的,由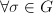 ,
,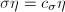 ,可知
,可知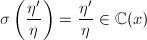 ,令
,令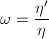 ,即得
,即得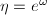 。
。 - 可假设
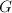 为
为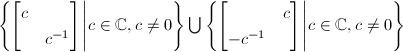 的子群,则
的子群,则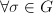 有
有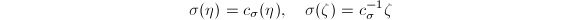 或者
或者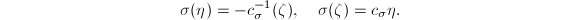 于是总有
于是总有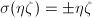 ,
,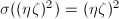 。由定理3可知必有
。由定理3可知必有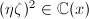 。设
。设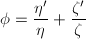 ,则
,则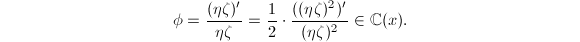 且由
且由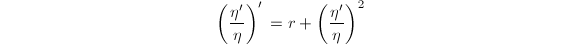 可计算得
可计算得
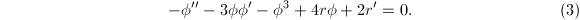 设
设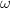 为方程
为方程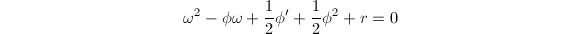 的一个解,对方程两端求导可得
的一个解,对方程两端求导可得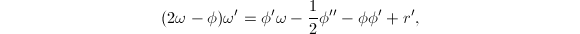 从而
从而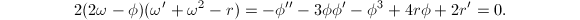 可假定
可假定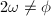 (这是第一类情形),于是有
(这是第一类情形),于是有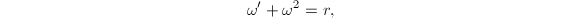 令
令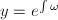 即为原方程的解,且
即为原方程的解,且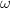 为
为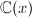 上的二次代数元。
上的二次代数元。 - 只须证扩张次数
![$[L:K]$](./latex/latex2png-DifferentialEquation_15763791_-5.gif) 有限即可。由于
有限即可。由于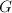 为有限群,可设
为有限群,可设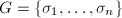 。取
。取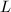 中的
中的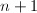 个元素
个元素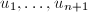 ,令
,令
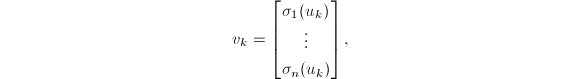 则必存在
则必存在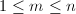 使得
使得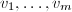 线性无关,
线性无关,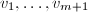 在
在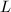 上线性相关。设
上线性相关。设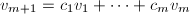 ,则
,则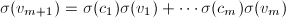 ,而由于
,而由于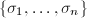 在任一个
在任一个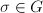 作用下仍为
作用下仍为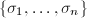 的一个排列,故由
的一个排列,故由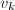 的构造知道
的构造知道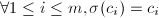 ,由定理3知
,由定理3知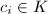 ,从而任
,从而任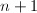 个
个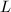 中的元素在
中的元素在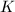 上线性相关,
上线性相关,![$[L:K]$](./latex/latex2png-DifferentialEquation_15763791_-5.gif) 自然是有限的。
自然是有限的。 - 由于对二阶线性方程来说,如果有一个Liouville解的话,那么所有解都是Liouville的。由Lie-Kolchin定理4可知在这种情况下
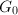 是可解的。但
是可解的。但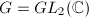 对应的
对应的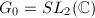 是不可解的。这个矛盾便证明了方程无Liouville解。
是不可解的。这个矛盾便证明了方程无Liouville解。
证毕。 □
在知道了Liouville解的形式之后,对Liouville解的存在性的判定便有了一些依据。下面的必要条件主要是通过对解的奇点分析得到的。我们知道,设![]() ,其中
,其中![]() ,
,![]() 为互素的多项式,则
为互素的多项式,则![]() 的极点即为
的极点即为![]() 的零点,且在极点
的零点,且在极点![]() 处的阶数等于
处的阶数等于![]() 作为
作为![]() 零点的重数。
零点的重数。![]() 在
在![]() 处阶数定义为
处阶数定义为![]() 。这实际上是更一般的离散赋值的特殊情形。
。这实际上是更一般的离散赋值的特殊情形。
在这样的定义下,![]() 在
在![]() 处的极点阶数实际上等于
处的极点阶数实际上等于![]() 。
。
 的所有极点阶数为偶数或1,在
的所有极点阶数为偶数或1,在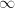 处的阶数为偶数或大于2;
处的阶数为偶数或大于2; 至少有一个极点的阶数为2或大于2的奇数;
至少有一个极点的阶数为2或大于2的奇数; 在极点处的阶数小于等于2,在
在极点处的阶数小于等于2,在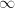 处的阶数大于等于2。可设部分分式分解
处的阶数大于等于2。可设部分分式分解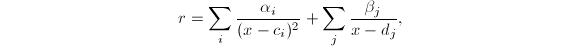 则
则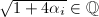 ,
,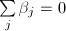 。令
。令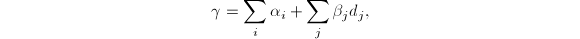 有
有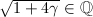 。
。
- 不妨设0为极点,考虑
 和
和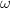 在0处的Laurent展式(其它点处类似考虑)
在0处的Laurent展式(其它点处类似考虑)
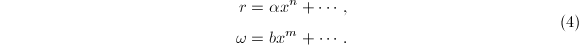 由
由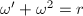 可得
可得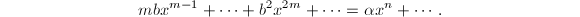 从而
从而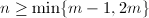 。故当
。故当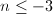 时,必有
时,必有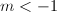 ,
,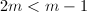 ,知
,知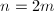 。所以极点阶数为偶数或者1。再考虑作为
。所以极点阶数为偶数或者1。再考虑作为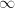 处的Laurent展式(4),则有
处的Laurent展式(4),则有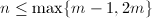 。故当
。故当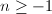 时,必有
时,必有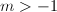 ,
,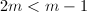 ,知
,知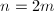 。所以
。所以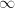 处的阶数为偶数或大于2。
处的阶数为偶数或大于2。 - 由
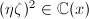 但
但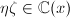 (否则为第一类情形),不失一般性,可设
(否则为第一类情形),不失一般性,可设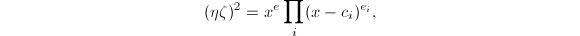 其中
其中 为奇数。则
为奇数。则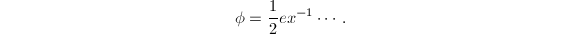 由式(3)及展式(4)可得
由式(3)及展式(4)可得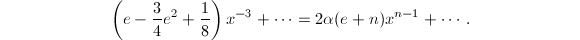 而
而 为奇数,
为奇数,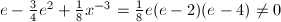 ,可知
,可知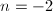 或
或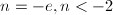 。所以
。所以 至少有一个极点阶数为2或为大于2的奇数。
至少有一个极点阶数为2或为大于2的奇数。 - 不妨设0为一个极点(其它极点类似考虑),由于解为
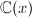 上的代数函数,可设在0处的Puiseux展式
上的代数函数,可设在0处的Puiseux展式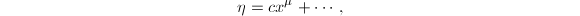 其中
其中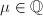 ,由
,由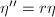 及展式(4)可得
及展式(4)可得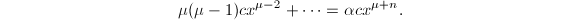 可知
可知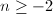 ,即
,即 在极点处的阶数小于等于2。并且若
在极点处的阶数小于等于2。并且若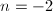 则有
则有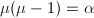 ,可知
,可知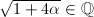 。于是可设
。于是可设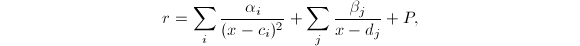 其中
其中![$P\in\mathbb{C}[x]$](./latex/latex2png-DifferentialEquation_16341323_-5.gif) 。再考虑
。再考虑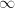 处
处 的Laurent展式(为了不混淆,我们将
的Laurent展式(为了不混淆,我们将 的系数换一个记号)
的系数换一个记号)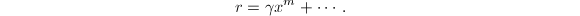 同样可得
同样可得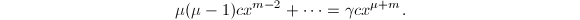 可知
可知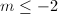 ,
,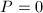 ,即有
,即有 在
在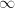 处的阶数大于等于2。由
处的阶数大于等于2。由
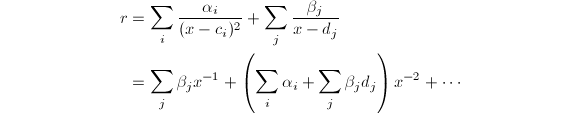 可知
可知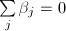 ,
,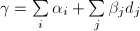 。再由
。再由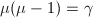 知
知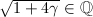 。
。
证毕。 □
下面我们来说明如何通过类似的奇点分析具体构造出所需要的Liouville解。首先设![]() 满足第一类必要条件,即
满足第一类必要条件,即![]() 的所有极点阶数为偶数或1,在
的所有极点阶数为偶数或1,在![]() 处的阶数为偶数或大于2。
处的阶数为偶数或大于2。
设解![]() ,
,![]() 。则
。则![]() 在
在![]() 处的部分分式项可写为
处的部分分式项可写为![]() 不妨仅考虑0处,简记
不妨仅考虑0处,简记![]() ,则
,则![]() 在0处的Laurent展式可写为
在0处的Laurent展式可写为![]() 其中
其中![]() 为
为![]() 的非负幂次项级数。以下分几种情况讨论。
的非负幂次项级数。以下分几种情况讨论。
(![]() ) 设0处极点阶数为1,
) 设0处极点阶数为1,![]() ,由
,由![]() 得到
得到![]() 可知
可知![]() ,
,![]() 。从而有
。从而有![]() 可知
可知![]() ,而0是极点,故只能有
,而0是极点,故只能有![]() 。从而
。从而![]() 在0处的部分分式为
在0处的部分分式为![]() 。为了统一起见,记
。为了统一起见,记![]() 。
。
(![]() ) 设0处极点阶数为2,
) 设0处极点阶数为2,![]() ,同样的推理可以得到
,同样的推理可以得到![]() ,
,![]() ,从而
,从而![]() 在0处的部分分式为
在0处的部分分式为![]() ,其中
,其中![]() 。
。
(![]() ) 设0处极点阶数为
) 设0处极点阶数为![]() ,可设
,可设![]() 由
由![]() 可得
可得![]() 。设
。设![]() 在0处的部分分式为
在0处的部分分式为![]() ,经过计算可得
,经过计算可得![]() ,其中
,其中![]() 为
为![]() 中
中![]() 的系数。
的系数。
(![]() ) 设0非极点,与(c1)同样的推理可得
) 设0非极点,与(c1)同样的推理可得![]() ,
,![]() 或
或![]() 。
。![]() 在0处的部分分式是0或者
在0处的部分分式是0或者![]() 。
。
综合以上四种情况得到![$$\omega=\sum_{c\in\Gamma}\left(s(c)[\sqrt{r}]_c+\frac{\alpha_c^{s(c)}}{x-c}\right)+\sum_{i=1}^d\frac{1}{x-d_i}+R,$$](./latex/latex2png-DifferentialEquation_172656637_.gif) 其中
其中![]() 表示
表示![]() 的极点集合,
的极点集合,![]() ,记号
,记号![]() 可取
可取
![]() 或
或![]() 。因此下面的任务就是确定
。因此下面的任务就是确定![]() ,
,![]() 和
和![]() 了,为此我们还需考虑
了,为此我们还需考虑![]() 在
在![]() 处Laurent展式
处Laurent展式![]()
(![]() ) 设
) 设![]() 处阶数为
处阶数为![]() 大于2,
大于2,![]() 代入
代入![]() 可得
可得![]() ,
,![]() 或
或![]() 。
。
(![]() ) 设
) 设![]() 处阶数为2,
处阶数为2,![]() ,同样的可得
,同样的可得![]() ,
,![]() ,
,![]() 。
。
(![]() ) 设
) 设![]() 处阶数为
处阶数为![]() ,
,![]() 表示
表示![]() 在
在![]() 处展式的多项式部分。类似(
处展式的多项式部分。类似(![]() )可得
)可得![]() ,
,![]() ,其中
,其中![]() 为
为![]() 中
中![]() 的系数。
的系数。
综合以上三条可得到![$$\omega=\underbrace{\sum_{c\in\Gamma}\left(s(c)[\sqrt{r}]_c+\frac{\alpha_c^{s(c)}}{x-c}\right)+s(\infty)[\sqrt{r}]_\infty}_\theta+\underbrace{\sum_{i=1}^d\frac{1}{x-d_i}}_{P'/P}.$$](./latex/latex2png-DifferentialEquation_117389319_.gif) 再比较两边
再比较两边![]() 展式的
展式的![]() 的系数可得
的系数可得![]() 最后还需要确定
最后还需要确定![]() ,设
,设![]() ,则
,则![]() 可写为
可写为![]() ,代入
,代入![]() 得到
得到![]() 用待定系数法求出多项式
用待定系数法求出多项式![]() 即可。得解
即可。得解![]() 。
。
以上对构造第一类解的讨论,我们可以稍作一些总结。为了求解![]() ,首先通过奇点分析得到
,首先通过奇点分析得到![]() (即每个奇点贡献的总和),再通过待定系数法求解关于多项式
(即每个奇点贡献的总和),再通过待定系数法求解关于多项式![]() 的一个微分方程,最后根据
的一个微分方程,最后根据![]() 和
和![]() 计算
计算![]() 。在构造另外两类解时过程也大抵如此,只不过奇点分析更复杂一些,关于
。在构造另外两类解时过程也大抵如此,只不过奇点分析更复杂一些,关于![]() 的微分方程次数会较高,而通过
的微分方程次数会较高,而通过![]() 和
和![]() 计算
计算![]() 的过程也更复杂,需要解一个代数方程。我们不再一一详述,具体可参见[10],不过为了完整起见,这里给出Saunder[11]对Kovacic算法的一个简化版本,不仅利于实现,也避免了具体求出所有奇点。
的过程也更复杂,需要解一个代数方程。我们不再一一详述,具体可参见[10],不过为了完整起见,这里给出Saunder[11]对Kovacic算法的一个简化版本,不仅利于实现,也避免了具体求出所有奇点。
- 预处理与必要条件检测。
- 设
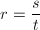 为既约分式,作无平方分解
为既约分式,作无平方分解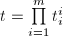 。
。 - 构造
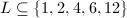 为
为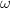 在
在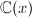 上代数次数可能的取值。
上代数次数可能的取值。
- 若
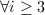 为奇数有
为奇数有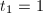 ,且
,且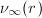 大于2或为偶数,则
大于2或为偶数,则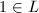 ;
; - 若
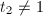 ,或
,或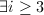 为奇数有
为奇数有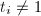 ,则
,则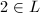 ;
; - 若
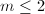 且
且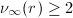 ,则
,则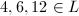 。
。
- 若
- 设
- 构造
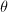 和
和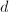 的组成部分。
的组成部分。
- 构造固定部分
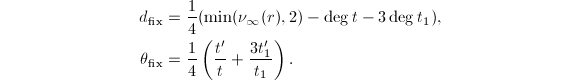
- 构造2阶极点对应项。设
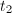 的根为
的根为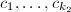 ,设
,设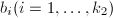 为
为 中
中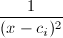 的系数,令
的系数,令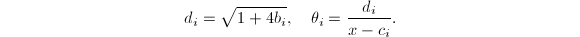
- 构造大于等于3阶极点对应项。当
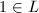 时求得
时求得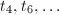 的根为
的根为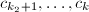 。设在
。设在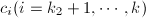 处的阶数为
处的阶数为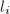 ,设
,设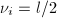 ,
,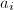 为
为![$[\sqrt{r}]_{c_i}$](./latex/latex2png-DifferentialEquation_85014615_-5.gif) 中
中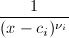 的系数,
的系数,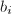 为
为![$r-[\sqrt{r}]_{c_i}^2$](./latex/latex2png-DifferentialEquation_36128449_-6.gif) 中
中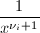 的系数。令
的系数。令![$$d_i=\frac{b_i}{a_i},\quad\theta_i=2[\sqrt{r}]_{c_i}+\frac{d_i}{x-c_i}.$$](./latex/latex2png-DifferentialEquation_50542683_.gif)
- 构造
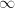 处阶数为2的对应项。若
处阶数为2的对应项。若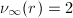 ,令
,令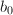 为
为 中
中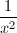 的系数,令
的系数,令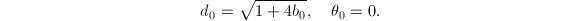
- 构造
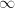 处阶数小于2的对应项。若
处阶数小于2的对应项。若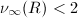 ,设
,设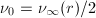 ,
,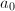 为
为![$[\sqrt{r}]_\infty$](./latex/latex2png-DifferentialEquation_38815498_-5.gif) 中
中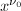 的系数,
的系数,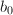 为
为![$r-[\sqrt{r}]_\infty^2$](./latex/latex2png-DifferentialEquation_56187738_-5.gif) 中
中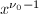 的系数,令
的系数,令![$$d_0=\frac{b_0}{a_0},\quad\theta_0=2[\sqrt{r}]_\infty.$$](./latex/latex2png-DifferentialEquation_69661571_.gif)
- 构造固定部分
- 构造
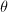 和
和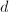 。
。
- 取
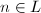 ,若
,若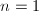 则
则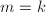 ,否则
,否则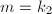 。
。 - 其中任取
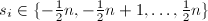 ,令
,令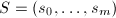 。构造
。构造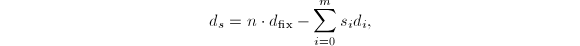
- 若
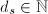 ,则令
,则令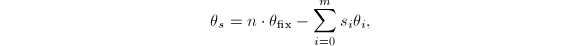 进行第四步的求解,否则换一组不同的
进行第四步的求解,否则换一组不同的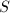 。若已尝试所有
。若已尝试所有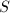 则换一个不同的
则换一个不同的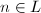 ,若已尝试所有的
,若已尝试所有的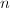 ,则算法终止。
,则算法终止。
- 取
- 求解。记
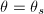 。
。
- 若
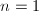 ,求解
,求解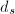 次首一多项式
次首一多项式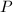 ,使
,使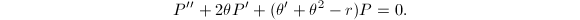 输出解
输出解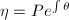 。
。 - 若
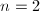 ,求解
,求解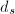 次首一多项式
次首一多项式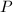 ,使
,使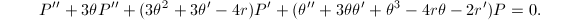 令
令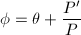 ,求解方程
,求解方程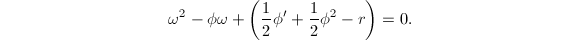 输出解
输出解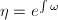 。
。 - 若
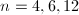 ,求解
,求解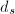 次首一多项式
次首一多项式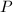 ,使
,使
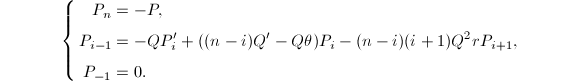 其中
其中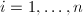 ,
,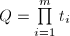 。求解方程
。求解方程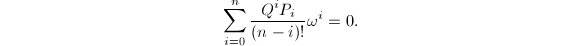 输出解
输出解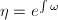 。
。
- 若
 高阶线性微分方程的多项式解和有理解
高阶线性微分方程的多项式解和有理解
Kovacic算法成功地解决了二阶线性方程的Liouville解,我们看到了微分Galois理论的巨大威力。尽管更加困难,使用微分Galois理论也可以的确用来求解高阶线性微分方程。例如早在1981年Singer[12]就在理论上提出了一个确定性的过程来求出所有的Liouville解,在此基础上还有许多发展,但复杂度仍太高以至于无法实际应用。因此需要考虑更快速、便于实现的方法。这里我们简要地介绍Abramov,Kvansenko[13],Bronstein[14]提出的高阶线性方程多项式解、有理解、原函数指数解的方法。
 多项式解
多项式解
在本节中设![]() 为一个数域,我们
为一个数域,我们![]() 上考虑
上考虑![]() 阶线性方程
阶线性方程
![]() 其中系数
其中系数![]() ,我们第一步的目标是求出方程(5)在
,我们第一步的目标是求出方程(5)在![]() 中的多项式解。设
中的多项式解。设![]() 为一个多项式解,代入方程(5)得到
为一个多项式解,代入方程(5)得到
![]() 记
记![]() ,设
,设![]() 在
在![]() 处取到
处取到![]() 。记
。记![]() 其中
其中![]() 表示
表示![]() 的首项系数。则
的首项系数。则![]() ,可知当
,可知当![]() 时,式(6)中左端最高次项为
时,式(6)中左端最高次项为![]() 比较式(6)两段最高项可知或者
比较式(6)两段最高项可知或者![]() ,或者
,或者![]() 。从而我们得到了
。从而我们得到了![]() 次数的上界
次数的上界![]() 其中
其中![]() 表示
表示![]() 的最大正整数根。
的最大正整数根。
如同我们经常做的,在得到![]() 次数上界之后便可用待定系数法求解
次数上界之后便可用待定系数法求解![]() 了,最终的未定系数便为解表达式中的任意常数。但由于无法精确求出
了,最终的未定系数便为解表达式中的任意常数。但由于无法精确求出![]() ,只能采取近似的估计,而估计的
,只能采取近似的估计,而估计的![]() 往往会很大,计算复杂度就较高。可以考虑如下的递推方法来求解关于待定系数的线性方程组更有效。
往往会很大,计算复杂度就较高。可以考虑如下的递推方法来求解关于待定系数的线性方程组更有效。
对“截断”的线性方程![]() (
(![]() ),同样定义如上的
),同样定义如上的![]() 和
和![]() ,记为
,记为![]() 和
和![]() (从而
(从而![]() ,
,![]() )。假设我们搜索次数不超过
)。假设我们搜索次数不超过![]() 的多项式解,同样比较首项系数可得
的多项式解,同样比较首项系数可得
![]() 从而求出
从而求出![]() ,再作变量替换
,再作变量替换![]() ,得到新的关于
,得到新的关于![]() 的方程
的方程![]() 再继续求解此方程不超过
再继续求解此方程不超过![]() 次的多项式解,如此续行即可。
次的多项式解,如此续行即可。
当然在通过(7)计算![]() 的过程中要考虑
的过程中要考虑![]() 的情形,若此时等式右端为零,则判定此方程无多项式解;若等式右端为零,则
的情形,若此时等式右端为零,则判定此方程无多项式解;若等式右端为零,则![]() 可视为一个未定参数,代入变换后的新方程进行计算。接下来当比较系数时,若等式左端为零,而右端含未定参数时,便可消去右端的某个参数。到求得
可视为一个未定参数,代入变换后的新方程进行计算。接下来当比较系数时,若等式左端为零,而右端含未定参数时,便可消去右端的某个参数。到求得![]() 之后,最终可以得到一个其系数中含若干个参数的多项式,将所有系数联立为零,可确定参数的值或者最终出现在解中的可变常数。这最后一个问题的规模是
之后,最终可以得到一个其系数中含若干个参数的多项式,将所有系数联立为零,可确定参数的值或者最终出现在解中的可变常数。这最后一个问题的规模是![]() 的[13],复杂度比非递推的待定系数法要小很多。
的[13],复杂度比非递推的待定系数法要小很多。
 有理解
有理解
设![]() 为有理函数解,则从方程(5)可知
为有理函数解,则从方程(5)可知![]() 的每一个极点都是
的每一个极点都是![]() 的零点,从而
的零点,从而![]() 的每个不可约因子都是
的每个不可约因子都是![]() 的因子。为了确定
的因子。为了确定![]() ,只需确定
,只需确定![]() 的各个不可约因子在
的各个不可约因子在![]() 中出现的次数即可。
中出现的次数即可。
设![]() 为
为![]() 的一个极点,
的一个极点,![]() 。设
。设![]() 在
在![]() 处的阶数为
处的阶数为![]() ,即
,即![]() ,
,![]() 。则有
。则有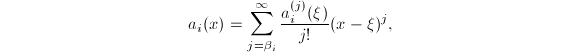 代入方程(5)得到
代入方程(5)得到
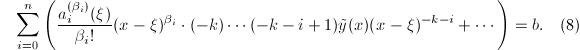 和多项式解情形类似的,我们定义
和多项式解情形类似的,我们定义![]() ,并设
,并设![]() 在
在![]() 处取到
处取到![]() 。记
。记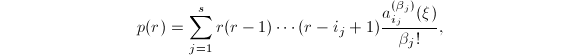 则当
则当![]() 时,式(8)左端
时,式(8)左端![]() 项的系数为
项的系数为![]() ,而
,而![]() ,可知必有
,可知必有![]() 。于是得到
。于是得到![]() 即为
即为![]() 在
在![]() 中的次数上界,其中
中的次数上界,其中![]() 表示
表示![]() 的最小负整数根。
的最小负整数根。
因此本质上和多项式解情形一样(对![]() 的分析变为了对
的分析变为了对![]() 的分析),我们从理论上得到了一个求有理函数的方法(求得分母,待定分子系数)。但在
的分析),我们从理论上得到了一个求有理函数的方法(求得分母,待定分子系数)。但在![]() 上分解系数
上分解系数![]() 总是不很方便的。为了合并
总是不很方便的。为了合并![]() 的乘积,从而将所有运算都限制在系数域
的乘积,从而将所有运算都限制在系数域![]() 中,我们引入如下平衡分解的概念(见[15])就显得很自然了。
中,我们引入如下平衡分解的概念(见[15])就显得很自然了。
再设![]() ,称
,称![]() 关于
关于![]() 是平衡的,若
是平衡的,若![]() 对于每个
对于每个![]() 都是平衡的。称
都是平衡的。称![]() 为关于
为关于![]() 的平衡分解,若此分解对于每个
的平衡分解,若此分解对于每个![]() 都是平衡分解。
都是平衡分解。
![]() 的无平方分解总是关于
的无平方分解总是关于![]() 的平衡分解,选取不同的
的平衡分解,选取不同的![]() ,可以得到不同于
,可以得到不同于![]() 的无平方分解的平衡分解。不严格地说,平衡分解要比无平方分解来得“细”,但比完全分解来得“粗”。我们可以只动用
的无平方分解的平衡分解。不严格地说,平衡分解要比无平方分解来得“细”,但比完全分解来得“粗”。我们可以只动用![]() 上的GCD运算,构造出
上的GCD运算,构造出![]() 关于
关于![]() 的平衡分解,为了不偏离主题太远,算法将在稍后给出。
的平衡分解,为了不偏离主题太远,算法将在稍后给出。
设![]() 为关于
为关于![]() 的平衡分解。考虑
的平衡分解。考虑![]() (
(![]() ),设
),设![]() 为在
为在![]() 上的完全分解。由于
上的完全分解。由于![]() 关于
关于![]() 平衡,故对于每个
平衡,故对于每个![]() ,
,![]() 在因子
在因子![]() 处的阶数都是相等的,公共的阶数可记为
处的阶数都是相等的,公共的阶数可记为![]() 。同样定义
。同样定义![]() ,并设
,并设![]() 在
在![]() 处取到
处取到![]() 。令
。令![$$p(r,x)=\sum_{j=1}^sr(r-1)\cdots(r-i_j+1)\frac{a_{i_j}^{(\beta_j)}(x)}{\beta_j!}\in K[r][x],$$](./latex/latex2png-DifferentialEquation_260795567_.gif) 为了得到
为了得到![]() 中
中![]() 的次数上界,可对
的次数上界,可对![]() 与
与![]() 施行Euclid算法,求出
施行Euclid算法,求出![]() 为使
为使![]() 的最小负整数值,则不难知道
的最小负整数值,则不难知道![]() 中
中![]() 的次数
的次数![]() 有上界
有上界![]()
这样我们避开了![]() 上的分解而求出了
上的分解而求出了![]() 的分母。可设
的分母。可设![]() ,
,![]() (
(![]() 为次数上界)。代入原方程(5)整理可得
为次数上界)。代入原方程(5)整理可得
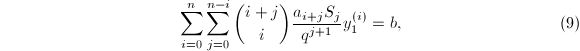 其中
其中![]() 接下来的问题就是求新方程(9)的多项式解
接下来的问题就是求新方程(9)的多项式解![]() ,而这是我们已经解决了的。
,而这是我们已经解决了的。
 平衡分解
平衡分解
我们在求高阶线性方程的有理解过程中引入了平衡分解的概念,其实也不难构造计算平衡分解的算法。我们将分几步走,每步的正确性都是不难验证的。
上面的两个算法都假定了![]() 无平方因子,因此平衡分解中因子的次数都是1。下面明显的定理给出一个最终版的平衡分解算法。
无平方因子,因此平衡分解中因子的次数都是1。下面明显的定理给出一个最终版的平衡分解算法。
 高阶线性微分方程的指数解
高阶线性微分方程的指数解
高阶Liouville解的求解要比二阶困难得多。1992年,Bronstein[14]提出了求解所有指数解(严格来说是原函数的指数解,即解![]() 满足
满足![]() ,
,![]() 为一个数域)的一组基的方法,并且此方法也已在Axiom系统上实现。此算法在[16]的基础上作了一些改进,甚至不需要在
为一个数域)的一组基的方法,并且此方法也已在Axiom系统上实现。此算法在[16]的基础上作了一些改进,甚至不需要在![]() 上分解
上分解![]() ,因此也可作为高阶线性微分方程的Singer一般算法[12]一个高效的子算法实现。
,因此也可作为高阶线性微分方程的Singer一般算法[12]一个高效的子算法实现。
在本节中仅考虑高阶![]() 阶齐次方程的情形,即
阶齐次方程的情形,即
![]()
 Riccati指数与Riccati界
Riccati指数与Riccati界
设![]() 为方程(10)的一个指数解。在
为方程(10)的一个指数解。在![]() 的情形,对方程
的情形,对方程![]() 我们知道
我们知道![]() 满足
满足![]() 这被称为原方程关联的Riccati方程。对一般的方程(10),不难求出对应的关联Riccati方程为
这被称为原方程关联的Riccati方程。对一般的方程(10),不难求出对应的关联Riccati方程为
![]() 其中
其中![]() 因此求指数解的问题就相当于求解非线性的关联Riccati方程在
因此求指数解的问题就相当于求解非线性的关联Riccati方程在![]() 中的解
中的解![]() 。
。
在这些精巧的定义下,Bronstein证明了以下关于解![]() 结构的定理[15]。
结构的定理[15]。
我们这里只能暂时省略论证的过程,来看看有了定理9之后能做些什么。首先,我们可以通过计算平衡分解计算得到![]() 。接下来可以通过试探依次求出
。接下来可以通过试探依次求出![]() 中求和的每一项组成部分。例如我们试探
中求和的每一项组成部分。例如我们试探![]() 为求和中的一项,令
为求和中的一项,令![]() ,
,![]() ,则由
,则由![]() 及
及![]() (
(![]() 为微分算子)可得
为微分算子)可得
![]() 且计算可得
且计算可得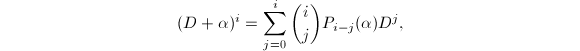 可得为新的关于
可得为新的关于![]() 的
的![]() 阶线性方程,如此续行直到求出解或者全部试探完毕。
阶线性方程,如此续行直到求出解或者全部试探完毕。
 多项式部分
多项式部分
首先我们考虑求出多项式部分![]() 。记
。记![]() ,利用
,利用![]() 中
中![]() 的最高次项为
的最高次项为![]() ,记
,记![]() 且在
且在![]() 处取到等号,设
处取到等号,设![]() 比较方程(11)两边
比较方程(11)两边![]() 的最高项可知
的最高项可知![]() 。从[16]命题2.3的证明可以知道
。从[16]命题2.3的证明可以知道![]() ,可知
,可知![]() 的取值只有有限多种,而
的取值只有有限多种,而![]() 的根只有有限多个,从而
的根只有有限多个,从而![]() 的取值至多只有有限多种可能,依次试探并作变量替换
的取值至多只有有限多种可能,依次试探并作变量替换![]() ,如此续行,直到求出所有可能的多项式解的集合。
,如此续行,直到求出所有可能的多项式解的集合。
 有理部分
有理部分
考虑![]() 对应项
对应项![]() 。简记
。简记![]() ,
,![]() ,
,![]() ,作部分分式分解
,作部分分式分解![]() 记
记![]() 且
且![]() 处取到等号。令
处取到等号。令![]() 其中
其中
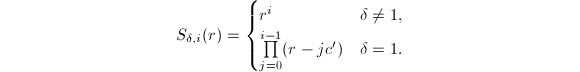 则比较方程(11)分母中的
则比较方程(11)分母中的![]() 的最高次项可知
的最高次项可知![]() 。由
。由![]() 可得到一个关于
可得到一个关于![]() 系数的代数方程组,得到的
系数的代数方程组,得到的![]() 至多有有限种可能。接下来依次求
至多有有限种可能。接下来依次求![]() 并试探所有的
并试探所有的![]() 对应的项,直到求出所有可能的
对应的项,直到求出所有可能的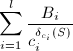 。
。
最后求解对数导数![]() 了,而这相当于对变换后的
了,而这相当于对变换后的![]() 阶线性方程(12)求多项式解
阶线性方程(12)求多项式解![]() ,是我们已经解决的问题。
,是我们已经解决的问题。
 二阶微分方程的特殊函数解
二阶微分方程的特殊函数解
许多特殊函数往往来源于某一类微分方程的解(二阶的尤为常见)。当一个方程没有Liouville解时,我们期望能够用特殊函数来表示方程的解,便于进一步的研究。精确地说,希望找到形如![]() 的解,其中
的解,其中![]() 为
为![]() 上的Liouville函数,
上的Liouville函数,![]() 为有理函数,
为有理函数,![]() 则为某一个标准方程的解(例如Bessel方程
则为某一个标准方程的解(例如Bessel方程![]() )。
)。
 变量替换
变量替换
下面我们考虑二阶方程![]() ,
,![]() 的特殊函数解。设给出特殊函数的标准方程为
的特殊函数解。设给出特殊函数的标准方程为![]() 作变量替换
作变量替换![]() ,记
,记![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,利用
,利用![]() ,
,![]() ,可得
,可得
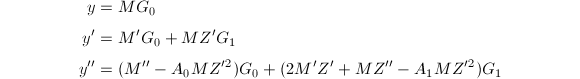 消去
消去![]() ,
,![]() 可得
可得
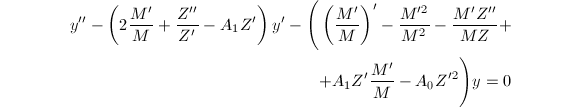 若
若![]() 满足待求解方程
满足待求解方程![]() ,则有
,则有
![]() 及
及![]() 可解得
可解得
![]() 代入式(13)可得
代入式(13)可得
![]()
 有理函数
有理函数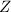 的求解
的求解
首先注意到,由式(14)可得![]() 为Liouville函数。因此要求得符合标准方程的解,关键问题如何找出合适的有理函数
为Liouville函数。因此要求得符合标准方程的解,关键问题如何找出合适的有理函数![]() 。寻找的主要方法还是分析函数的奇异性,首先求出
。寻找的主要方法还是分析函数的奇异性,首先求出![]() 的分母
的分母![]() ,再找到其分子次数的上界,最后通过求解代数方程求出分子的各系数。
,再找到其分子次数的上界,最后通过求解代数方程求出分子的各系数。
设![]() ,下证必有
,下证必有![]() 。由于
。由于![]() ,可得
,可得![]() ,
,![]() (当
(当![]() )或
)或![]() (当
(当![]() 时),
时),![]() ,
,![]() ,同样由
,同样由![]() 及式(15)可得
及式(15)可得![]() 即
即![]() 再注意到
再注意到![]() 可得所要证的。
可得所要证的。
最后注意当![]() 时有
时有![]() ,从而
,从而![]() ,故不等号成立与后一种情形是重合的,这就完成了证明。
□
,故不等号成立与后一种情形是重合的,这就完成了证明。
□
由此我们得到了想要的![]() 的表达式和
的表达式和![]() 次数的上界,将
次数的上界,将![]() 的系数待定代入(15)可以得到一个代数方程组,最后解此方程组即可。另外,为保证得到的
的系数待定代入(15)可以得到一个代数方程组,最后解此方程组即可。另外,为保证得到的![]() 不是常数(注意常数总是解),我们可以添加额外的一些限制方程。设
不是常数(注意常数总是解),我们可以添加额外的一些限制方程。设![]() ,
,![]() ,,
,,![]() ,加入方程
,加入方程![]() ,其中
,其中![]() 为新的待定元。可以看出,解新的方程组可以保证至少有一个
为新的待定元。可以看出,解新的方程组可以保证至少有一个![]() 使得
使得![]() ,从而
,从而![]() 非常数。
非常数。
函数![]() ,
,![]() 也允许带上参数(例如Bessel方程中的参数
也允许带上参数(例如Bessel方程中的参数![]() ),将它们也视作方程组中的未定元,求解代数方程组时可以将参数确定下来。
),将它们也视作方程组中的未定元,求解代数方程组时可以将参数确定下来。
 经典特殊函数
经典特殊函数
在本节的最后我们给出定理10在一些经典特殊函数的情形,便于实际应用。
- Airy函数,由方程
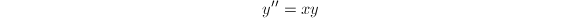 给出。
给出。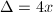 ,
,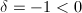 ,可知
,可知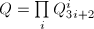 ,
,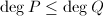 或
或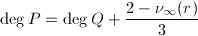 ,
,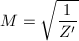 。
。 - Bessel函数,由方程
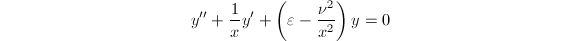 给出,其中
给出,其中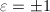 。
。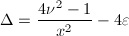 ,
,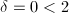 ,可知
,可知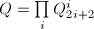 ,
,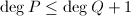 或
或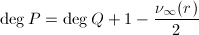 ,
,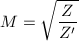 。
。 - Kummer函数,由方程
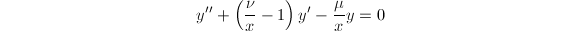 给出。
给出。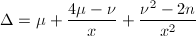 ,
,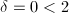 ,可知
,可知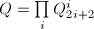 ,
,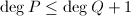 或
或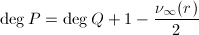 ,
,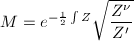 。
。 - Whittaker函数,由方程
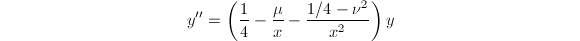 给出,
给出,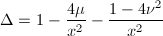 ,
,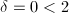 ,可知
,可知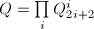 ,
,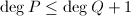 或
或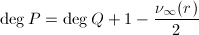 ,
,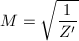 。
。
参考文献
[1]Computer algebra: systems and algorithms for algebraic computation, Academic Press, London, UK, 1988.
[2]The Problem of Integration in Finite Terms, Transactions of the American Mathematical Society 139 (1969), 167-189.
[3]Integration of elementary functions, Journal of Symbolic Computation 9 (1990), no.2, 117 - 173.
[4]A new algorithm for the integration of Exponential and Logarithmic Functions, Proceedings of the 1977 MACSYMA Users Conference (1977), 263-274.
[5]The Risch differential equation problem, SIAM Journal on Computing 15 (1986), no.4, 903 - 918.
[6]Integration of Algebraic Functions, Ph.D thesis, Dpt. of EECS, Massachusetts Institute of Technology (1984).
[7]Intégration algorithmique des fonctions élémentairement transcendantes sur une courbe algébrique, Annales de l'institut Fourier 34 (1984), no.2, 271-276.
[8]常微分方程教程, 高等教育出版社, 北京, 2004.
[9]Galois theory of linear differential equations, 科学出版社, 北京, 2007.
[10]An algorithm for solving second order linear homogeneous differential equations, Journal of Symbolic Computation 2 (1986), no.1, 3 - 43.
[11]An implementation of Kovacic's algorithm for solving second order linear homogeneous differential equations, Proceedings of the fourth ACM symposium on Symbolic and algebraic computation (1981), 105-108.
[12]Liouvillian Solutions of n-th Order Homogeneous Linear Differential Equations, American Journal of Mathematics 103 (1981), no.4, 661-682.
[13]Fast algorithms to search for the rational solutions of linear differential equations with polynomial coefficients, Proceedings of the 1991 international symposium on Symbolic and algebraic computation (1991), 267 - 270.
[14]Linear ordinary differential equations: breaking through the order 2 barrier, Papers from the international symposium on Symbolic and algebraic computation (1992), 42 - 48.
[15]On solutions of linear ordinary differential equations in their coefficient field, Journal of Symbolic Computation 13 (1992), no.4, 413 - 439.
[16]Liouvillian solutions of linear differential equations with Liouvillian coefficients, Journal of Symbolic Computation 11 (1991), no.3, 251 - 273.
[17]Solutions of linear ordinary differential equations in terms of special functions, Proceedings of the 2002 international symposium on Symbolic and algebraic computation (2002), 23-28.
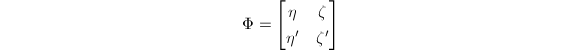 故Picard-Vessiot域为
故Picard-Vessiot域为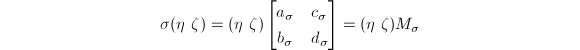 其中
其中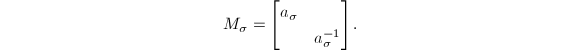 可知
可知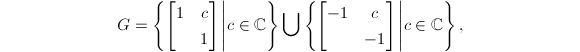 的确也是
的确也是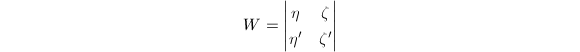 为Wronsky行列式,由于
为Wronsky行列式,由于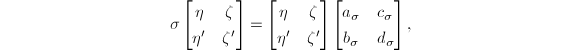 可知
可知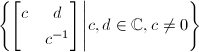 的子群,即
的子群,即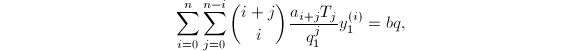 其中
其中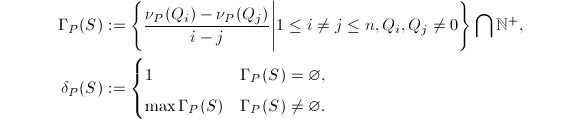
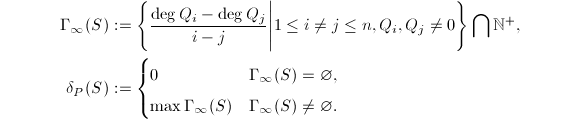
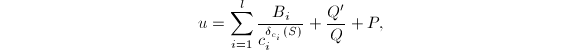 其中
其中