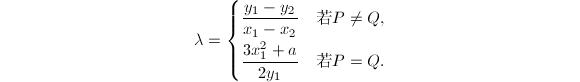相对于素数判定来说,因子分解的实现就没办法达到那么快速了。因子分解至今仍没有类似于素数判定的多项式算法,这也成为了RSA公钥系统安全得以保障的基础。鉴于这两个问题的难度相差较大,在我们施行分解之前,最好是预先知道目标整数的确不是一个素数,否则很可能花费了很大力气只干了素数判定的活——杀鸡用牛刀了。
因子分解的分为一般方法和特殊方法两大类,通常倾向于先针对数的特殊性(例如![]() )使用特殊方法,如果目标数的形式不那么特殊,再尝试使用一般方法。当然,前者往往要比后者快上许多。
)使用特殊方法,如果目标数的形式不那么特殊,再尝试使用一般方法。当然,前者往往要比后者快上许多。
我们这里着重介绍因子分解的一般方法,且总是用![]() 表示待分解的目标数。特殊方法可以以后视实际情况逐渐加入。
表示待分解的目标数。特殊方法可以以后视实际情况逐渐加入。
 试除法
试除法
无论素数判定还是因子分解,试除法(Trial Division)都是首先要进行的步骤。在试除的策略上有两种不同的选择:
- 用足够大的空间来储存试除用的素数因子(储存方法可以相当紧凑,比如用
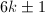 对应的0-1向量表示的大整数)。
对应的0-1向量表示的大整数)。 - 不耗费大量空间来储存所有需要的素因子,这时需要一个快速生成素数的子程序,或者干脆只用2,3以及
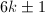 型的整数来作为试除因子。
型的整数来作为试除因子。
很少发生一个数没有小因子的情况,例如根据Mertens定理[1],奇数中没有![]() 以下因子的比例
以下因子的比例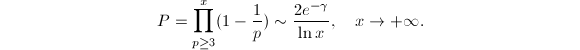 可以知道76%的奇数都有小于100的素因子,而没有小于
可以知道76%的奇数都有小于100的素因子,而没有小于![]() 因子的奇数比例仅为6.1%[2]。因此在大多数情况,试除法的第二种选择已经足够,实现却是最为简单的。
因子的奇数比例仅为6.1%[2]。因此在大多数情况,试除法的第二种选择已经足够,实现却是最为简单的。
 Euclid算法
Euclid算法
Euclid算法用于因子分解也非常简单。我们预先计算好小于100的素数之积![]() 然后将
然后将![]() 与目标数
与目标数![]() 进行Euclid算法,最终得到
进行Euclid算法,最终得到![]() 与
与![]() 的最大公因子,继续分解公因子就可以得到在100以下的因子分解了。同样可以预先计算出100到200,200到300的素数乘积
的最大公因子,继续分解公因子就可以得到在100以下的因子分解了。同样可以预先计算出100到200,200到300的素数乘积![]() ,
,![]() 等等。这本质上是试除法的一个实现,当
等等。这本质上是试除法的一个实现,当![]() 非常大时,必须借助高精度算术来进行
非常大时,必须借助高精度算术来进行![]() 除以
除以![]() 的操作,因此频繁的试除会十分耗时,而Euclid方法可以施行很少次数,再在机器精度上完成最终的分解,提高效率。
的操作,因此频繁的试除会十分耗时,而Euclid方法可以施行很少次数,再在机器精度上完成最终的分解,提高效率。
 Pollard
Pollard 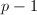 方法
方法
Pollard ![]() 方法由Pollard于1974年提出,其基本想法是这样的:设素数
方法由Pollard于1974年提出,其基本想法是这样的:设素数![]() ,由Fermat小定理,又有
,由Fermat小定理,又有![]() ,因此
,因此![]() 就可能是
就可能是![]() 的一个非平凡因子。当然,问题在于我们并不知道
的一个非平凡因子。当然,问题在于我们并不知道![]() 是多少。一个合理的假设是
是多少。一个合理的假设是![]() 的因子都很小,比如说,
的因子都很小,比如说,![]() 所有素因子都包含在因子基
所有素因子都包含在因子基![]() 中,我们来尝试着找到一个
中,我们来尝试着找到一个![]() 能够“覆盖”
能够“覆盖”![]() ,即是说
,即是说![]() ,从而
,从而![]() ,因此我们可以转而求
,因此我们可以转而求![]() 来获得所要的非平凡因子。例如设素因子上限为
来获得所要的非平凡因子。例如设素因子上限为![]() ,便可以简单的取
,便可以简单的取![]() 或是最小公倍数
或是最小公倍数![]() .
.
下面给出Pollard ![]() 方法的一个版本:
方法的一个版本:
- 设素因子搜索的上限为
 ,生成
,生成 以下的形如
以下的形如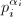 数对应的素数因子之表
数对应的素数因子之表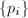 ,即:2,3,2,5,7,2,3,11,13,2...
,即:2,3,2,5,7,2,3,11,13,2... - 随机选择正整数
 ,顺次计算
,顺次计算
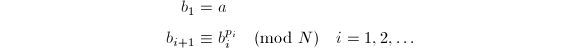
- 定期检查(例如每当
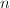 为20的倍数时)
为20的倍数时)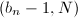 ,若
,若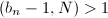 ,则得到一个
,则得到一个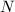 的因子;否则继续第2步中的递推计算。
的因子;否则继续第2步中的递推计算。
 Pollard
Pollard 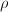 方法
方法
目前几乎所有实用的分解方法都是概率性的算法,目标是找到能计算![]() 的算法,使得
的算法,使得![]() 的概率较大(而最大公因子可以很快地计算)。上面的Pollard
的概率较大(而最大公因子可以很快地计算)。上面的Pollard ![]() 就是一例,下面即将看到的Pollard
就是一例,下面即将看到的Pollard ![]() 方法也不例外。
方法也不例外。
Pollard ![]() 方法由Pollard在1975年提出,它来自一个有趣的事实:随机选取大约
方法由Pollard在1975年提出,它来自一个有趣的事实:随机选取大约![]() 个整数(
个整数(![]() 为一个常数),就有很大概率在这些整数中找到两个是
为一个常数),就有很大概率在这些整数中找到两个是![]() 同余的。实践中可以采用同余递推序列
同余的。实践中可以采用同余递推序列![]() 来产生伪随机数,其中
来产生伪随机数,其中![]() 为映射:
为映射:![]() 。设
。设![]() 是
是![]() 的一个因子,且找到
的一个因子,且找到![]() ,则计算
,则计算![]() 便可能得到
便可能得到![]() 的一个非平凡因子。
的一个非平凡因子。
 |
| Pollard $\rho$ 方法 |
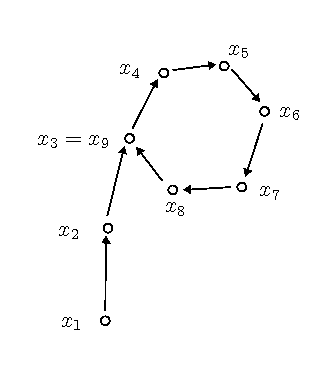
由![]() 的有限性,如上定义的一阶的递推序列
的有限性,如上定义的一阶的递推序列![]() 在
在![]() 意义下必定是最终循环的(如图,看上去就像希腊字母
意义下必定是最终循环的(如图,看上去就像希腊字母![]() )。设其开头的非循环部分长度为
)。设其开头的非循环部分长度为![]() ,循环节长度为
,循环节长度为![]() 。著名的Floyd算法可以在
。著名的Floyd算法可以在![]() 步内高效地找出序列中的两个重复元素,并且只用常数的储存空间。
步内高效地找出序列中的两个重复元素,并且只用常数的储存空间。
实践中常采用的![]() 为
为![]() 选择二次的递推序列一方面能提供足够的随机性,另一方面计算起来也非常简便。
选择二次的递推序列一方面能提供足够的随机性,另一方面计算起来也非常简便。
 平方型分解(SQUFOF)
平方型分解(SQUFOF)
平方型分解(SQUare FOrm Factorization)是由Shanks在大约三十前发展的算法,但他从来没有正式发表过[6]。尽管SQUFOF复杂度为![]() 也是一个指数级的算法(而下面介绍的CFRAC, ECM, QS等都是次指数级的),但其仍有自身的优势:一方面算法十分简洁优美、便于实现(甚至可以在袖珍计算器上实现),并且在
也是一个指数级的算法(而下面介绍的CFRAC, ECM, QS等都是次指数级的),但其仍有自身的优势:一方面算法十分简洁优美、便于实现(甚至可以在袖珍计算器上实现),并且在![]() 到
到![]() 范围的整数分解仍然是最快的。
范围的整数分解仍然是最快的。
SQUFOF依赖于对二次域结构的分析,我们在这里仅给出算法的描述,略去证明,具体可参见[6]:
 连分式方法(CFRAC)
连分式方法(CFRAC)
连分式方法(Continued FRACtion)是由Morrison和Brillhart于1975年提出的[7],他们运用此方法成功地分解了Fermat数![]() 。它以及之后要介绍的二次筛(QS)以及数域筛(NFS)都基于如下一个简单的事实:如果
。它以及之后要介绍的二次筛(QS)以及数域筛(NFS)都基于如下一个简单的事实:如果![]() 则
则![]() 就是
就是![]() 的一个非平凡因子。
的一个非平凡因子。
当然,寻找这样的![]() 不能只靠运气,CFRAC方法构造一组同余式
不能只靠运气,CFRAC方法构造一组同余式
![]() 其中
其中![]() 都是因子基
都是因子基![]() 中较小的素数。如果找到足够多这样的同余式(例如个数
中较小的素数。如果找到足够多这样的同余式(例如个数![]() ),那么利用二元域
),那么利用二元域![]() 上的Gauss消元法,可以找到组合系数
上的Gauss消元法,可以找到组合系数![]() 使得
使得![]() 我们记
我们记![]() 此时若令
此时若令
![]() 便则有我们所需要的
便则有我们所需要的![]()
如何构造这么多同余式呢?我们知道用连分式部分展式可以得到二次无理数![]() (
(![]() )的好的有理数逼近。设
)的好的有理数逼近。设![]() 为其近似分数,那么
为其近似分数,那么![]() 的绝对值就很小,从而
的绝对值就很小,从而![]() 很可能在因子基
很可能在因子基![]() 下分解,同时
下分解,同时![]() ,便能得到我们所期望的同余式(1)。
,便能得到我们所期望的同余式(1)。
- 选择适当的
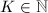 (通常取为1,当连分式展式周期太小而无法产生足够的同余式时选择另一个
(通常取为1,当连分式展式周期太小而无法产生足够的同余式时选择另一个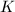 ),令
),令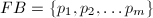 ,使得
,使得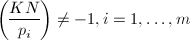 。
。 - 计算
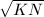 的连分式展式,得到一系列近似分式
的连分式展式,得到一系列近似分式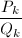 。
。 - 计算
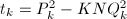 ,尝试在
,尝试在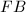 下得到
下得到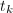 的分解,若分解成功则有
的分解,若分解成功则有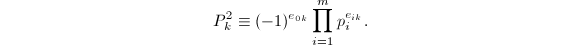
- 当得到足够多的同余式时(
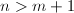 即可),用
即可),用 上的Gauss消元法得到(2)中的
上的Gauss消元法得到(2)中的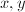 。
。 - 若
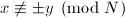 ,输出
,输出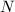 的非平凡因子
的非平凡因子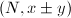 。
。
 Lenstra椭圆曲线方法(ECM)
Lenstra椭圆曲线方法(ECM)
因子分解说到底就是寻找![]() ,使得
,使得![]() 非平凡,关键在于提高寻找的
非平凡,关键在于提高寻找的![]() 的成功率。Pollard
的成功率。Pollard ![]() 方法通过计算
方法通过计算![]() 来提高成功率,实质上是在群
来提高成功率,实质上是在群![]() 中考虑问题。椭圆曲线方法(Elliptic Curve Method)转而在有限域上随机的椭圆曲线群中考虑问题。由于椭圆曲线可以有许多不同的选择,ECM方法要比Pollard
中考虑问题。椭圆曲线方法(Elliptic Curve Method)转而在有限域上随机的椭圆曲线群中考虑问题。由于椭圆曲线可以有许多不同的选择,ECM方法要比Pollard ![]() 高效许多,到目前为止是第三快的因子分解方法,仅次于数域筛和二次筛。
高效许多,到目前为止是第三快的因子分解方法,仅次于数域筛和二次筛。
首先我们给出域上椭圆曲线的定义:
椭圆曲线既是代数曲线又是一个加法群:
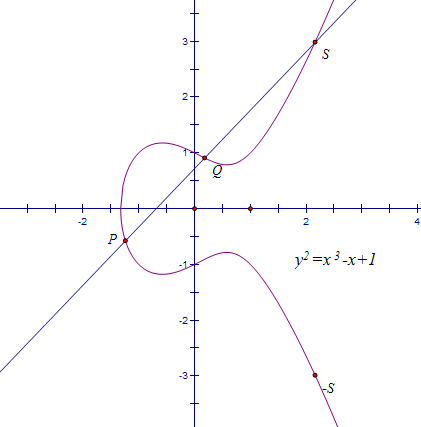 |
| 椭圆曲线 |
由定义通过简单的计算我们可以得到:
上面我们考虑了域上的椭圆曲线,然而对于因子分解的任务来说,我们需要考虑![]() 上的椭圆曲线。由于
上的椭圆曲线。由于![]() 等在
等在![]() 中未必可逆,此时上面的加法运算未必能定义好,不过这无关紧要,例如当
中未必可逆,此时上面的加法运算未必能定义好,不过这无关紧要,例如当![]() 不可逆时,我们已经可以通过计算
不可逆时,我们已经可以通过计算![]() 来得到
来得到![]() 的非平凡因子,从而直接完成分解的目标;而当
的非平凡因子,从而直接完成分解的目标;而当![]() 可逆时,一切可以正常按照上面的显式表达进行运算。因此在这里我们不再花功夫用严格的语言来定义
可逆时,一切可以正常按照上面的显式表达进行运算。因此在这里我们不再花功夫用严格的语言来定义![]() 上的椭圆曲线了。
上的椭圆曲线了。
下面我们将Pollard ![]() 中类似的想法用在椭圆曲线中。
中类似的想法用在椭圆曲线中。
Pollard ![]() 方法的实质就是期望整数
方法的实质就是期望整数![]() 足够光滑而能在因子基
足够光滑而能在因子基![]() 下分解。和Pollard
下分解。和Pollard ![]() 方法中的想法类似,ECM中首先从椭圆曲线
方法中的想法类似,ECM中首先从椭圆曲线![]() 中随机取一点
中随机取一点![]() ,我们期望
,我们期望![]() 的阶
的阶![]() 是足够光滑的,从而可以在
是足够光滑的,从而可以在![]() 下分解,然后通过加法规则计算
下分解,然后通过加法规则计算![]() (当然我们预先并不知道
(当然我们预先并不知道![]() ),利用计算过程中出现的不可逆元,求得
),利用计算过程中出现的不可逆元,求得![]() 的一个因子。
的一个因子。
- 随机选取整数
 ,
,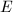 为曲线
为曲线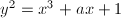 。
。 - 设
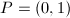 ,
,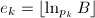 ,根据式(3)递推地计算
,根据式(3)递推地计算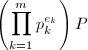 。若计算过程中出现不可逆元
。若计算过程中出现不可逆元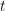 ,则到第三步,否则到第一步。
,则到第三步,否则到第一步。 - 计算
 。如果
。如果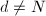 则输出
则输出 ,算法终止;如果
,算法终止;如果 则到第一步。
则到第一步。
下面我们谈一下搜索极限![]() 的取法,和Pollard
的取法,和Pollard ![]() 方法中一样,我们需要知道有限域
方法中一样,我们需要知道有限域![]() 上群
上群![]() 的阶,下面有限域上椭圆曲线最主要的定理归功于Hasse,告诉我们群
的阶,下面有限域上椭圆曲线最主要的定理归功于Hasse,告诉我们群![]() 的阶在
的阶在![]() 左右[9]:
左右[9]:
下面的定理则给出了关于光滑性的一个估计[9]:
由上面两个定理我们可以得到选取![]() 的一些信息,设素数
的一些信息,设素数![]() ,而
,而![]() ,由定理1和2知道平均要试
,由定理1和2知道平均要试![]() 条曲线可以得到一个阶为
条曲线可以得到一个阶为![]() -光滑的椭圆曲线,算法7计算总共需要
-光滑的椭圆曲线,算法7计算总共需要![]() 个群运算,为使运算量最小,因此可取
个群运算,为使运算量最小,因此可取![]() 。实践中
。实践中![]() 的选择依赖于时间的承受限度,例如我们将搜索的素数因子限制在
的选择依赖于时间的承受限度,例如我们将搜索的素数因子限制在![]() 以下,那么可取
以下,那么可取![]() (接近
(接近![]() )。
)。
由上面的讨论可以看出,ECM的时间复杂度依赖于![]() 的最小素因子
的最小素因子![]() 而非
而非![]() 本身(为
本身(为![]() ),因此很适宜在试除法和Pollard
),因此很适宜在试除法和Pollard ![]() 方法之后用ECM来找出较小的因子(10-20个十进制位左右)。
方法之后用ECM来找出较小的因子(10-20个十进制位左右)。
ECM算法的效率很大程度取决于群运算的快慢,最关键的是模![]() 的求逆运算。我们在本节最后给出Montgomery的一个加速算法,使得我们能够同时对多条椭圆曲线进行求逆运算。
的求逆运算。我们在本节最后给出Montgomery的一个加速算法,使得我们能够同时对多条椭圆曲线进行求逆运算。
- 递推计算
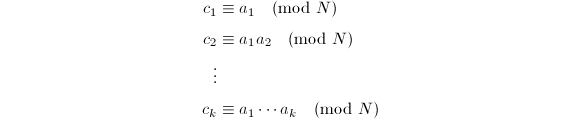
- 施行一次扩展Euclid算法求出
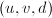 满足
满足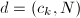 ,
,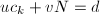 。
。
- 若
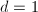 ,则
,则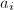 均有逆,到第三步;
均有逆,到第三步; - 若
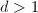 ,依次计算
,依次计算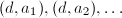 直到
直到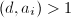 ,输出
,输出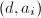 为
为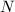 的一个非平凡因子。
的一个非平凡因子。
- 若
- 递推计算逆
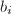 并输出:
并输出:
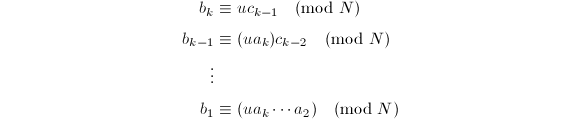
 二次筛法(QS)
二次筛法(QS)
二次筛法(Quadratic Seive)是由Pomerance于1981年提出的,直到1993年是世界上渐进最快的通用大整数因子分解方法,第一的位置后来被数域筛所取代,不过对于120位以下的整数,二次筛还是要比数域筛快一些。
 单个多项式二次筛法(SPQS)
单个多项式二次筛法(SPQS)
正如我们在CFRAC方法中提到的,QS方法也要构造一组同余式(1),但通过筛法避免了其中![]() 在因子基
在因子基![]() 下的分解,而这种分解在不存在的情况下常常会大量消耗时间。设
下的分解,而这种分解在不存在的情况下常常会大量消耗时间。设![]() ,若
,若![]() ,则不难验证对于任意
,则不难验证对于任意![]() ,也有
,也有![]() 。于是我们找到了一系列数都有因子
。于是我们找到了一系列数都有因子![]() ,这样一个事实构成了QS方法的基础。
,这样一个事实构成了QS方法的基础。
我们取![]() ,为了使其与某个
,为了使其与某个![]() 模
模![]() 同余,且尽可能小以便在
同余,且尽可能小以便在![]() 下分解,考虑二次多项式
下分解,考虑二次多项式![]() ,
,![]() ,则
,则![]() 且
且![]() 为
为![]() 的阶,符合我们的要求。接下来是筛法的过程:对于
的阶,符合我们的要求。接下来是筛法的过程:对于![]() 中满足搜索极限
中满足搜索极限![]() 的素数
的素数![]() 及幂次
及幂次![]() ,首先求解方程
,首先求解方程![]() ,其解数(如果有解的话)
,其解数(如果有解的话)
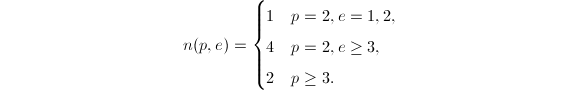 并且解都可以快速地求得。对方程的任一个解
并且解都可以快速地求得。对方程的任一个解![]() ,令
,令![]() ,则有
,则有![]() 。给定一个搜索区间
。给定一个搜索区间![]() (通常很长),则对任意与
(通常很长),则对任意与![]() 差
差![]() 的整数倍的
的整数倍的![]() ,
,![]() 都有因子
都有因子![]() 。可用一张表储存区间
。可用一张表储存区间![]() 中每个整数对应的因子,当对所有
中每个整数对应的因子,当对所有![]() 与
与![]() 进行如上过程后,通过检查表,即可得到许多
进行如上过程后,通过检查表,即可得到许多![]() 中在
中在![]() 下完全分解的整数了。接下来的步骤则与CFRAC的后半部分完全相同。
下完全分解的整数了。接下来的步骤则与CFRAC的后半部分完全相同。
 多个多项式二次筛法(MPQS)
多个多项式二次筛法(MPQS)
MPQS是对上述只用一个二次多项式的SPQS方法的一个改进,使用更多的二次多项式来减小![]() 的值,从而减小
的值,从而减小![]() 的大小和搜索区间的长度。考虑
的大小和搜索区间的长度。考虑![]() 形式的多项式(
形式的多项式(![]() ),配方得
),配方得![]() ,因此可选取系数使
,因此可选取系数使![]() ,设
,设![]() ,则
,则![]() 。我们需要
。我们需要![]() 尽可能的小,设搜索区间的长度
尽可能的小,设搜索区间的长度![]() ,自然的把
,自然的把![]() 的中心设置在
的中心设置在![]() 的极小点
的极小点![]() 处,此时
处,此时![]() 且
且![]() 在
在![]() 上的最大值与最小值之差为
上的最大值与最小值之差为![]() 从而宜取
从而宜取![]() ,且
,且![]() 接近
接近![]() 。因此选择系数的过程可以如下进行
。因此选择系数的过程可以如下进行
- 选择区间长度
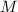 。
。 - 选择接近于
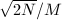 的素数
的素数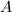 。
。 - 求解
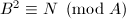 (例如利用Shanks算法3)。
(例如利用Shanks算法3)。 - 令
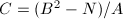 。
。
接下来的步骤便是对这样选取的多个多项式进行筛法,最终得到足够多的同余式进行![]() 上的Gauss消元法。
上的Gauss消元法。
 数域筛法(NFS)
数域筛法(NFS)
数域筛法(Number Field Sieve)是目前渐进最快的通用因子分解方法,其时间复杂度为![]() ,其中常数
,其中常数![]() 依赖于不同的算法实现。例如对于针对
依赖于不同的算法实现。例如对于针对![]() 形式整数的特殊数域筛法(SNFS)有
形式整数的特殊数域筛法(SNFS)有![]() ,而对于一般数域筛法(GNFS)有
,而对于一般数域筛法(GNFS)有![]() 。对于120位以上的大数,NFS是最强有力的分解算法。例如互联网上的分布式大整数分解项目NFSNet采用的便是此法。
。对于120位以上的大数,NFS是最强有力的分解算法。例如互联网上的分布式大整数分解项目NFSNet采用的便是此法。
参考文献
[1]素数论, 清华大学出版社, 北京, 2007.
[2]Prime Numbers and Computer Methods for Factorization, Boston; Basel; Stuttgart: Birkhäuser, 1985.
[3]A $p+1$ Method of Factoring, Mathematics of Computation 39 (1982), no.159, 225-234.
[4]Modern Computer Algebra, Cambridge University Press, 2002.
[5]An improved Monte Carlo factorization algorithm, BIT Numerical Mathematics 20 (1980), no.2, 176--194.
[6]Square form factorization, Mathematics of computation 77 (2008), no.261, 551-588.
[7]A Method of Factoring and the Factorization of $F_7$, Mathematics of Computation 29 (1975), no.129, 183-205.
[8]Asymptotically Fast Factorization of Integers, Mathematics of Computation 36 (1981), no.153, 255-260.
[9]A Course in Computational Algebraic Number Theory, Springer Verlag, 1993.
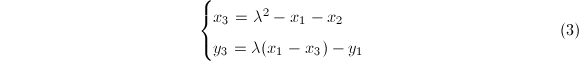 其中
其中