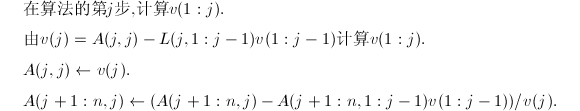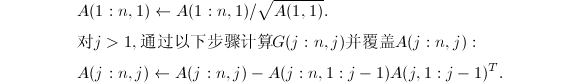数值分析的一个基本原则是:求解任何问题都应充分利用它的特殊的结构特性.在数值线性代数中,这意味着当问题中出现诸如对称性,定型性和稀疏性等特性时,需要将适用于求解一般矩阵的算法修改,使其效率更高.这将是本章的主题.我们的主要目的是设计一些特殊的![]() 分解的专用算法.
分解的专用算法.

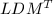 和
和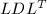 分解
分解
由前述![]() 分解容易证明以下的
分解容易证明以下的![]() 分解定理:
分解定理:
特别地,在![]() 为对称方阵的情形,成立以下
为对称方阵的情形,成立以下![]() 分解:
分解:
由以上定理可知,对对称阵施行![]() 或
或![]() 分解时,工作量可减半.在第
分解时,工作量可减半.在第![]() 步,由于
步,由于![]() 且假定
且假定![]() 的前
的前![]() 列已知,则
列已知,则![]() 也为已知.定义
也为已知.定义![]() 为
为![]() 的前
的前![]() 个分量,则
个分量,则
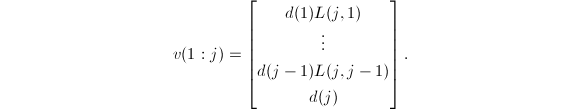 于是,向量
于是,向量![]() 可通过对
可通过对![]() 的第
的第![]() 行做简单数乘得到.由
行做简单数乘得到.由![]() 的第
的第![]() 个方程,有关系式
个方程,有关系式![]() .
.
相应地有以下算法:
本算法大约减少了一半的工作量,需要![]() 个flop.可以证明,当
个flop.可以证明,当![]() 对称且正定时,以上算法不但能够顺利执行完,而且非常稳定[1].如果
对称且正定时,以上算法不但能够顺利执行完,而且非常稳定[1].如果![]() 对称但非正定,则需要结合对称地选主元,即在算法的第
对称但非正定,则需要结合对称地选主元,即在算法的第![]() 步比较
步比较![]() 得到其中绝对值最大的元素并通过置换阵
得到其中绝对值最大的元素并通过置换阵![]() 的对称作用
的对称作用![]() 将其换到
将其换到![]() 位置,使之后的算法稳定执行.
位置,使之后的算法稳定执行.
 Cholesky分解
Cholesky分解
可以证明,若![]() 是正定的,则在
是正定的,则在![]() 的分解
的分解![]() 中,
中,![]() 的对角元均大于
的对角元均大于![]() .然而,仅仅存在
.然而,仅仅存在![]() 分解仍不足以保证分解算法的稳定性.
分解仍不足以保证分解算法的稳定性.
以下着重介绍对称正定阵的Cholesky分解.
我们下面导出一个含有大量Gaxpy运算的Cholesky分解算法.比较等式![]() 的第
的第![]() 列得到
列得到
![]() 也就是说,
也就是说,
![]() 如果
如果![]() 的第
的第![]() 列已知,则可计算出
列已知,则可计算出![]() .由上式中各元素间的相等关系推出
.由上式中各元素间的相等关系推出
![]() 于是得到以下算法:
于是得到以下算法:
本算法共需![]() 个flop.这一算法在
个flop.这一算法在![]() 正定时相当稳定.
正定时相当稳定.
 Vandemonde方程组
Vandemonde方程组
Vandemonde方程组与下一节将要讲到的正定对称的Toeplitz阵问题是两类重要的能在![]() 的计算量内稳定求解的问题.
的计算量内稳定求解的问题.
设![]() ,形如
,形如
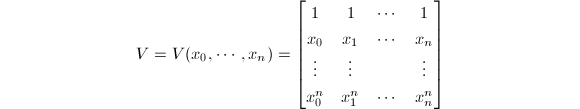 的矩阵
的矩阵![]() 被称作Vandemonde矩阵.下面我们讨论线性方程组
被称作Vandemonde矩阵.下面我们讨论线性方程组![]() 及
及![]() 的求解.
的求解.
Vandemonde矩阵与多项式插值有密切的联系.首先注意到,若有![]() ,并定义
,并定义![]() ,则对于
,则对于![]() ,
,![]() .故若
.故若![]() 是互异的,则可通过构造插值多项式
是互异的,则可通过构造插值多项式![]() 求解.
求解.
第一步是计算插值多项式![]() 的Newton表达式:
的Newton表达式:
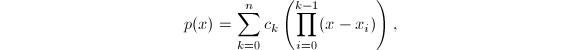 常数
常数![]() 是差商,可按以下步骤确定:
是差商,可按以下步骤确定:
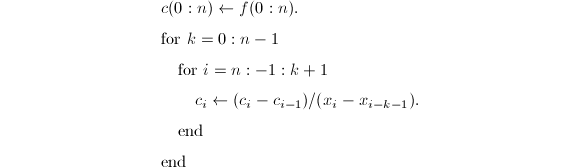 下一步是由
下一步是由![]() 产生
产生![]() .通过迭代
.通过迭代
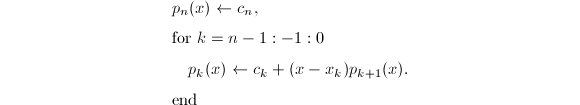 来定义多项式
来定义多项式![]() .可求得
.可求得![]() .于是系数
.于是系数![]() 可如下求得
可如下求得
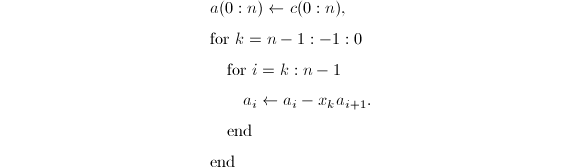 以上两步骤合并即得到求解
以上两步骤合并即得到求解![]() 的算法,共需
的算法,共需![]() 个flop.
个flop.
该算法事实上即多项式插值问题的一般算法.它事实上利用了如下分解
![]() 其中
其中
![\begin{displaymath}
L_k (\alpha)=
\left[\begin{array}{c|c}
I_k& O\\
\hline\\
O&
\begin{matrix}
1& \cdots& & O\\
-\alpha& \ddots\\
\vdots& \ddots& \ddots\\
0& \cdots&\ -\alpha& 1
\end{matrix}
\end{array}\right],
\end{displaymath}
\begin{equation*}
D_k=\mathrm{diag} (\underbrace{1,\cdots. 1}_{k+1},x_{k+1}-x_0,\cdots,x_n-x_{n-k-1}).
\end{equation*}](./latex/latex2png-SpecialLinearEquation_124182867_.gif) 于是对于方程组
于是对于方程组![]() ,只要利用
,只要利用![]() 即可得到其三角阵分解,从而求解方程组.
即可得到其三角阵分解,从而求解方程组.
 对称正定Toeplitz阵及相关问题
对称正定Toeplitz阵及相关问题
设![]() ,存在
,存在![]() 对所有
对所有![]() 和
和![]() 满足
满足![]() ,则
,则![]() 称为Toeplitz阵.Toeplitz阵属于一个更大的反向对称(persymmetric)矩阵类 (即沿反对角线进行"转置"不改变).容易验证,Toeplitz阵及非奇异Toeplitz阵的逆也是反向对称的.本节将利用这一特性给出对称正定Toeplitz阵的
称为Toeplitz阵.Toeplitz阵属于一个更大的反向对称(persymmetric)矩阵类 (即沿反对角线进行"转置"不改变).容易验证,Toeplitz阵及非奇异Toeplitz阵的逆也是反向对称的.本节将利用这一特性给出对称正定Toeplitz阵的![]() 的算法.不失一般性,以下均设
的算法.不失一般性,以下均设![]() .
.
 Yule-Walker问题的Durbin算法
Yule-Walker问题的Durbin算法
Yule-Walker问题是系数矩阵为Toeplitz阵![]() ,非齐次项
,非齐次项![]() 的线性方程组
的线性方程组![]() .可以看到,这种问题具有很大的特殊性,即它的非齐次项与系数矩阵有密切关系,但它是进一步讨论的基础.设我们已经求解了
.可以看到,这种问题具有很大的特殊性,即它的非齐次项与系数矩阵有密切关系,但它是进一步讨论的基础.设我们已经求解了![]() 阶的Yule-Walker方程组
阶的Yule-Walker方程组![]() .下面给出如何在
.下面给出如何在![]() 内求解
内求解![]() 阶Yule-Walker方程组,其中
阶Yule-Walker方程组,其中![]() 为
为![]() 阶反向置换阵:
阶反向置换阵:

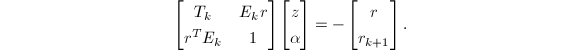 注意到
注意到
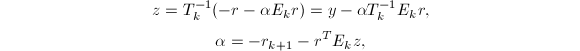 由于
由于![]() ,故有
,故有
![]() 代入
代入![]() 表达式
表达式
![]() 其中
其中![]() 是大于
是大于![]() 的,因Toeplitz阵
的,因Toeplitz阵![]() 为正定的:
为正定的:
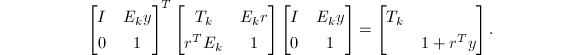 进一步利用
进一步利用![]() ,即得到完整的Durbin算法,需
,即得到完整的Durbin算法,需![]() 个flop.
个flop.
 一般右端向量的Levinson算法
一般右端向量的Levinson算法
可以用类似方法求解右端为任意向量的Toeplitz方程组![]() .
.
假设已解出![]() 阶Toeplitz方程组
阶Toeplitz方程组![]() ,现需求解
,现需求解
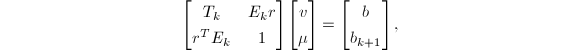 同时假定
同时假定![]() 阶Yule-Walker方程组
阶Yule-Walker方程组![]() 的解也已得到.由
的解也已得到.由![]() 可知
可知
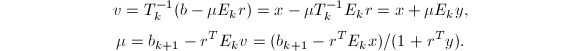 这样,我们可在
这样,我们可在![]() 个flop内完成
个flop内完成![]() 阶方程组的求解.全部算法共需
阶方程组的求解.全部算法共需![]() 个flop.
个flop.
 正定对称Toeplitz阵求逆Trench算法
正定对称Toeplitz阵求逆Trench算法
对称正定的Toeplitz阵![]() 的最令人吃惊的性质之一是它的逆可以在
的最令人吃惊的性质之一是它的逆可以在![]() 个flop内算出.为了得到这个算法,我们将
个flop内算出.为了得到这个算法,我们将![]() 做如下划分:
做如下划分:
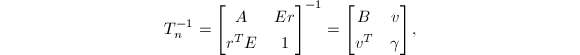 由
由
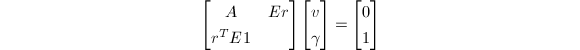 得到
得到
![]() 若
若![]() 是
是![]() 阶Yule-Walker方程组
阶Yule-Walker方程组![]() 的解,则
的解,则
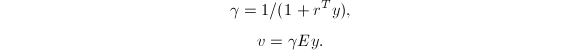 于是我们得到了
于是我们得到了![]() 的最后一列.
的最后一列.
因为![]() ,故
,故![]() .由于
.由于![]() 是非奇异的Toeplitz阵,其逆是反向对称的,于是
是非奇异的Toeplitz阵,其逆是反向对称的,于是
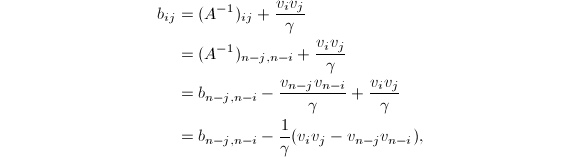 于是我们可以"从外向里"地确定
于是我们可以"从外向里"地确定![]() ,以
,以![]() 阶矩阵为例形象地描述如下:
阶矩阵为例形象地描述如下:
假定![]() 的最后一行和最后一列已知
的最后一行和最后一列已知
 这里
这里![]() 和
和![]() 分别代表未知元素和已知元素.交替利用
分别代表未知元素和已知元素.交替利用![]() 的反向对称性和前述递推式,可求出
的反向对称性和前述递推式,可求出![]() 的顺序子块
的顺序子块![]() 如下:
如下:
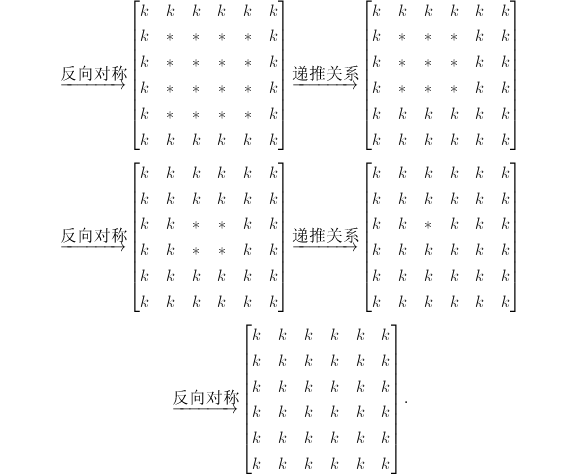 当然,当求解一个既对称又反对称的矩阵时,只需求解矩阵的"上楔形"即可,即
当然,当求解一个既对称又反对称的矩阵时,只需求解矩阵的"上楔形"即可,即
 由以上分析,不难得到对于
由以上分析,不难得到对于![]() 阶正定对称Toeplitz阵的求逆算法,称为Trench算法.它需要
阶正定对称Toeplitz阵的求逆算法,称为Trench算法.它需要![]() 个flop.
个flop.
Cybenko(1978)年对上述各算法做了误差分析,认为其稳定性与Cholesky方法相当.
最后指出,以上两节涉及到的Vandermonde矩阵和Toeplitz矩阵与快速Fourier变换(FFT)有密切的关系,使得特定形式的矩阵与向量乘法可以FFT速度计算。可参见[2]和[3].
参考文献
[2]矩阵计算, 科学出版社, 2001.
[3]Computational Frameworks for the Fast Fourier Transform, SIAM Publications, Philadelphia, PA, 1992.