隐藏目录
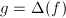 ,那么
,那么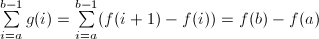 ,即
,即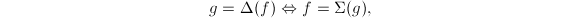 这和微积分的互逆定理
这和微积分的互逆定理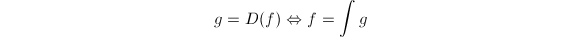 类似.
定义降阶乘
类似.
定义降阶乘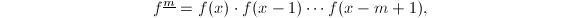 则
则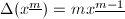 ,于是
,于是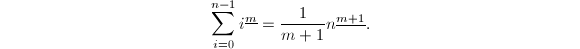 设
设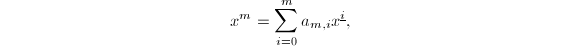 则
则
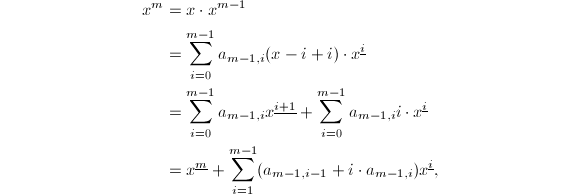 于是有递推公式
于是有递推公式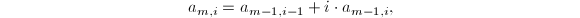 其中
其中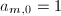 .
.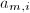 在组合数学中被称为第二类斯特林(Stirling)数,它表示将一个
在组合数学中被称为第二类斯特林(Stirling)数,它表示将一个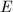 元有限集划分为
元有限集划分为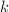 个非空子集的方法数.以
个非空子集的方法数.以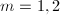 为例:
为例:
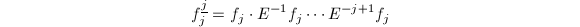 没有更小的降阶乘因子,因为如果
没有更小的降阶乘因子,因为如果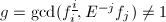 ,则
,则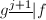 .
.
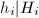 ,因此
,因此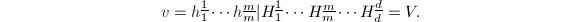 在算法实际运行过程中,一旦
在算法实际运行过程中,一旦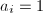 或
或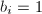 ,可以预计
,可以预计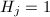 ,其中
,其中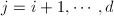 ,此时可以自动结束计算.
,此时可以自动结束计算.
 多项式级数
多项式级数
为了解决多项式级数求和问题,我们先来研究一元单项式级数求和.
事实上可以利用二项式展开求出任意次幂方和,但这样做得到的表达式一般比较复杂. 如果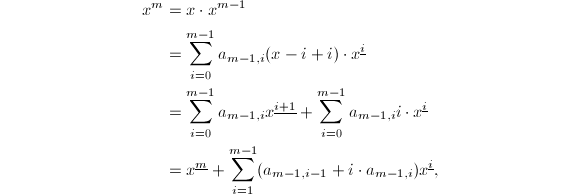 于是有递推公式
于是有递推公式设![]() ,则
,则
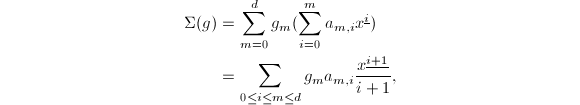 因此
因此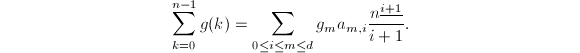
 超几何级数
超几何级数
和多项式级数的情形一样,首先研究一元超几何单项式级数求和.
- 二项式系数
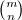 是超几何单项式,因为
是超几何单项式,因为
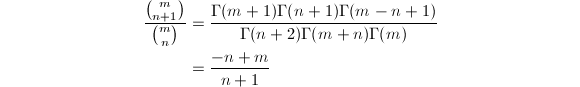
设![]() 并且满足
并且满足![]() ,
,![]() .设
.设![]() ,则
,则![]() ,
,![]() 令
令![]() ,则
,则![]() 即
即![]() ,所以存在
,所以存在![]() 使得
使得![]() ,其中
,其中![]()
 极大阶乘分解
极大阶乘分解
极大阶乘分解(Greatest Factorial Factorization)是多项式的一种特殊分解.
这样定义是为了保证根据极大阶乘分解的定义,它有很好的性质.
 Gosper算法
Gosper算法
在上面的讨论中,超几何单项式级数求和归结到求解超几何单项式的差分原函数.给定超几何单项式![]() ,设
,设![]() ,
,![]() ,则
,则
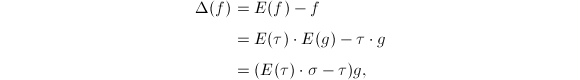 于是
于是![]() 由超几何单项式的性质可以设
由超几何单项式的性质可以设![]() ,
,![]() ,其中
,其中![]() ,并且
,并且![]() 均为首一多项式,上式化为
均为首一多项式,上式化为![]() 这样我们就把求解差分原函数的问题归结到求解多项式方程,理论上可以直接通过待定系数法像求解线性方程组一样解出这个方程来,但是计算量很大.
这样我们就把求解差分原函数的问题归结到求解多项式方程,理论上可以直接通过待定系数法像求解线性方程组一样解出这个方程来,但是计算量很大.
Gosper算法利用极大阶乘分解来求解这个多项式方程,记![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,方程两边同除以
,方程两边同除以![]() 得
得![]() 其中
其中![]() 于是有
于是有![]() 设
设![]() ,则
,则
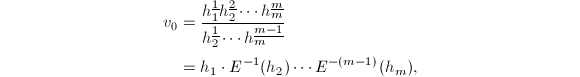
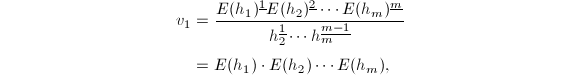 再由
再由![]() ,
,![]() 可得
可得![]() 若
若![]() ,则
,则
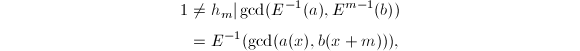 而这等价于
而这等价于![]() 我们可以写出求
我们可以写出求![]() 的某一个倍数
的某一个倍数![]() 的算法.
的算法.
现在我们将方程化成了![]() 其中
其中![]() 为已知的首一多项式.左右同除以
为已知的首一多项式.左右同除以![]() ,得
,得![]() 其中
其中![]() ,
,![]() ,
,![]() .设
.设![]() 其中
其中![]() 可以这样确定:
可以这样确定:
设![]() ,
,![]() 为
为![]() 中
中![]() 的系数.
的系数.
- 若
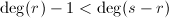 或
或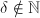 ,令
,令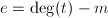 .
. - 若
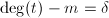 ,不可解.
,不可解. - 若
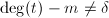 ,设
,设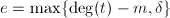 ,如果
,如果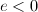 ,不可解.
,不可解.
比较对应项系数将得到一个上三角阵的线性方程组,这时就可以解出![]() 来.通过这一系列手续,最终求得
来.通过这一系列手续,最终求得![]()