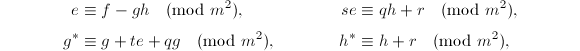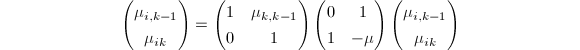事实上我们可以讨论UFD及其分式域上的多项式,但下面我们仅限于讨论![]() 和
和![]() 上的多项式。由相关的高等代数学的知识,我们知道对于
上的多项式。由相关的高等代数学的知识,我们知道对于![]() 上的多项式
上的多项式![]() ,其在
,其在![]() 中的不可约因子分解可对应于在
中的不可约因子分解可对应于在![]() 中的不可约因子分解,即若
中的不可约因子分解,即若![]() 则有
则有![]() 于是
于是![]() 上任一多项式
上任一多项式![]() 的因子分解对应于
的因子分解对应于![]() 上的因子分解和
上的因子分解和![]() 上本原多项式的因子分解。前者在素数理论中讨论,这里我们只讨论后者。
上本原多项式的因子分解。前者在素数理论中讨论,这里我们只讨论后者。
很自然的,由前面的最大公因子模方法我们可以想到用模方法来求解因子分解问题。首先我们可以利用上一章中的无平方因子分解的方法得到![]() 上的无平方因子本原多项式
上的无平方因子本原多项式![]() ,这时,我们会遇到如下一些问题:
,这时,我们会遇到如下一些问题:
- 素数
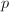 的选取要足够大,以使我们能从
的选取要足够大,以使我们能从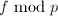 得到
得到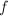 ,这一点我们可由模公因子算法中介绍的Mignotte界理论得到。
,这一点我们可由模公因子算法中介绍的Mignotte界理论得到。 - 虽然
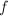 已是无平方因子,但
已是无平方因子,但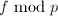 却不一定是无平方因子的。如多项式
却不一定是无平方因子的。如多项式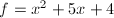 无平方因子,但
无平方因子,但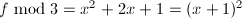 .那么在随机选取素数
.那么在随机选取素数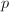 的时候如何使得
的时候如何使得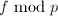 也是无平方因子呢?这一点在结式理论和后文中回答.
也是无平方因子呢?这一点在结式理论和后文中回答. - 当我们在
![$\mathbb{Z}_p[x]$](./latex/latex2png-PolyFacZ_71410771_-5.gif) 中将多项式分解后,如何将
中将多项式分解后,如何将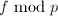 的分解对应到
的分解对应到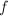 的分解。最简单的方法是尝试每一种可能的因子组合。因为若
的分解。最简单的方法是尝试每一种可能的因子组合。因为若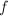 有不可约分解
有不可约分解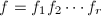 ,则
,则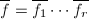 ,但
,但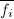 不一定不可约。当然,用这种尝试的方法有时效率很低,因此后面还要介绍一种格中短向量(short vectors in lattices)方法。
不一定不可约。当然,用这种尝试的方法有时效率很低,因此后面还要介绍一种格中短向量(short vectors in lattices)方法。
综上,我们首先要进入![]() 中求得因子分解,这一步我们可以利用“大素数”方法和“小素数”方法,只是这里的小素数不再是各不相同的素数,而是素数幂。第二步是由
中求得因子分解,这一步我们可以利用“大素数”方法和“小素数”方法,只是这里的小素数不再是各不相同的素数,而是素数幂。第二步是由![]() 返回
返回![]() 中,求得最终结果,可以用尝试因子组合的方法和格中短向量方法.
中,求得最终结果,可以用尝试因子组合的方法和格中短向量方法.
 大素数模方法和因子组合(Factor Combination)算法
大素数模方法和因子组合(Factor Combination)算法
由推论1知,![]() 是无平方因子的当且仅当
是无平方因子的当且仅当![]() .
.
由于![]() ,则我们有下面的:
,则我们有下面的:
假设有![]() 上本原多项式
上本原多项式![]() 的分解
的分解![]() ,且在模
,且在模![]() 下有:
下有:![]() 其中
其中![]() 为
为![]() 上首一不可约多项式.若
上首一不可约多项式.若![]() 比Mignotte界
比Mignotte界![]() 小,则有下面的等式:
小,则有下面的等式:![]() 该式原先在
该式原先在![]() 上就已成立了.其中指标集
上就已成立了.其中指标集![]() 为
为![]() .
.
输入:无平方因子![]() 次本原多项式
次本原多项式![]() ,其中
,其中![]() 且
且![]() ,
,
输出:![]() 在
在![]() 上的不可约因子
上的不可约因子![]() .
.
- 若
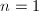 则输出
则输出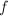 ,否则
,否则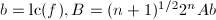 ,
, - 随机任取一个奇素数
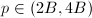 ,直至
,直至![$\gcd(\overline{f},\overline{f}')=1\in\field{p}[x]$](./latex/latex2png-PolyFacZ_16859241_-5.gif) ,即满足上面推论条件,
,即满足上面推论条件, - 利用有限域上因子分解算法求出
![$g_1,\ldots,g_r\in\mathbb{Z}[x]$](./latex/latex2png-PolyFacZ_95129026_-5.gif) ,其无穷范数均比
,其无穷范数均比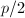 要小,且在
要小,且在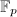 上不可约,于是
上不可约,于是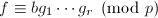 ,
, 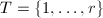 ,
,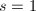 ,
,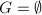 ,
,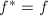 ,
,- 当
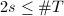 时循环执行下面4步,否则转第10步,
时循环执行下面4步,否则转第10步, - 枚举
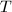 的所有
的所有 元子集
元子集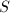 ,并做下两步7、8循环:
,并做下两步7、8循环: - 计算
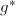 ,
,![$h^*\in\mathbb{Z}[x]$](./latex/latex2png-PolyFacZ_74668388_-5.gif) 使得其无穷范数比
使得其无穷范数比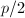 要小并且
要小并且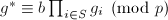 ,
,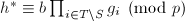 ,
, - 若
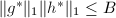 则
则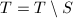 ,
,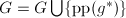 ,
,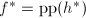 ,
,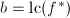 ,跳出6、7、8循环并转第5步,
,跳出6、7、8循环并转第5步, 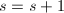 ,
,- 输出
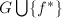 .
.
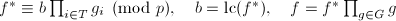 ,
,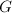 中多项式均不可约,
中多项式均不可约,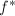 本原且它的任何一个不可约因子
本原且它的任何一个不可约因子![$u\in\mathrm{Z}[x]$](./latex/latex2png-PolyFacZ_16213090_-5.gif) 有
有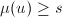 .
.
初始时命题显然成立,假设命题在每次循环进行到第7步前均是成立的,此时经过第7步后当第8步的条件成立时,各量均要发生变化,根据前面的分析则有![]() ,于是
,于是![]() 是
是![]() 的因子。由于
的因子。由于![]() 且对任何
且对任何![]() 的不可约因子
的不可约因子![]() 有
有![]() ,则
,则![]() 是
是![]() 的不可约因子.当
的不可约因子.当![]() 有一个不可约因子
有一个不可约因子![]() 满足
满足![]() 时,当循环到s时必然能将此因子选出,这一点可以构造来证明,即取指标集
时,当循环到s时必然能将此因子选出,这一点可以构造来证明,即取指标集![]() 为
为![]() 在
在![]() 中不可约因子的编号.
中不可约因子的编号.
最后一步是证明在第5步时,若![]() ,则
,则![]() 是不可约的.令
是不可约的.令![]() 是
是![]() 的一个不可约因子且
的一个不可约因子且![]() 非平凡,于是
非平凡,于是![]() .但是
.但是![]() ,且
,且![]() ,则
,则![]() 必为常数,
必为常数,![]() 必不可约.
□
必不可约.
□
首先![]() ,若取
,若取![]() ,则
,则
![]()
![]()
![]() 同样的取
同样的取![]() 时也可验证是不可以的。若取
时也可验证是不可以的。若取![]() ,则
,则
![]()
![]() 此时
此时![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,下一步
,下一步![]() ,循环条件不满足,则
,循环条件不满足,则![]() .
.
对于一般的多项式,我们可以如下分解.当然,在算法第4步分解无平方因子多项式时,也可以调用后面几节将要介绍的分解算法.
 Hensel提升(lifting)理论
Hensel提升(lifting)理论
以下我们全在整数环这个特殊的UFD中讨论,有些算法和命题在将![]() 换为其它的UFD,如
换为其它的UFD,如![]() 也是正确的。
也是正确的。
当我们已知一个分解![]() (
(![]() ,
,![]() 互素)时,最简单的问题是获得分解
互素)时,最简单的问题是获得分解![]() ,即将其“提升”。由于
,即将其“提升”。由于![]() 是素数,则存在
是素数,则存在![]() ,
,![]() 使得
使得![]() ,如果我们取:
,如果我们取:![]() 则有
则有
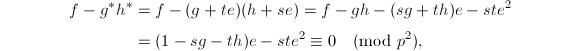 这样可以达到我们的要求。
这样可以达到我们的要求。
我们可以给出如下的单步Hensel提升(Hensel Step)算法.
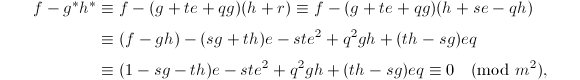 这是因为根据前面的引理我们由
这是因为根据前面的引理我们由由![]() 知
知![]() 也是首一的,且
也是首一的,且![]()
![]() 由
由![]() 也可得到
也可得到![]() ,于是
,于是![]() .
.
其次,![]() ,
,
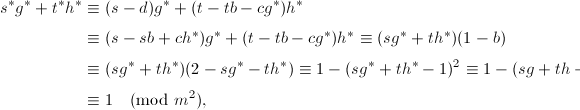 由
由![]() 可知
可知![]() ,于是
,于是![]()
![]() 而
而![]() ,于是
,于是![]() ,由
,由![]() 知
知![]() .所有结论证毕.
□
.所有结论证毕.
□
既然本节开始提出的方法已经能够解决问题,为什么还要引入上面的算法呢?我们通过下面一个例子来说明问题:
![]() 任取为
任取为![]() ,则对
,则对![]() 进行
进行![]() 的带余除法有:
的带余除法有:![]() 于是
于是![]() ,
,![]() ,故
,故![]()
![]()
![]()
![]()
![]()
![]()
正如Hensel单步提升算法所提到的,我们有![]() ,
,![]() .
.
如果我们归纳地利用单步Hensel算法,依次对![]() ,
,![]() ,
,![]() ,
,![]() 使用,则对任何正整数
使用,则对任何正整数![]() ,我们总可找到比其大的
,我们总可找到比其大的![]() 的幂次,于是有下面的:
的幂次,于是有下面的:
前面所说的均是二因子的Hensel提升,为了做多因子的情况,我们先给出如下定义:
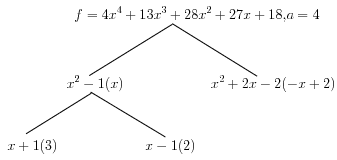 |
| 模5因子树 |
当然由模![]() 的因子树我们可以由单步Hensel算法得到模
的因子树我们可以由单步Hensel算法得到模![]() 乃至更高次幂的因子树,只要我们由根结点依次一步步在每个结点做Hensel提升即可.下面给出该算法:
乃至更高次幂的因子树,只要我们由根结点依次一步步在每个结点做Hensel提升即可.下面给出该算法:
输入:整数![]() 和
和![]() 次多项式
次多项式![]() ,
,![]() 使得
使得![]() ,正整数
,正整数![]() ,一个
,一个![]() 模
模![]() 的因子树
的因子树![]() ,共有
,共有![]() 个叶子.
个叶子.
输出:整数![]() 使得
使得![]() 和一个
和一个![]() 模
模![]() 的因子树
的因子树![]() ,各个新结点
,各个新结点![]() 和原结点
和原结点![]() 满足
满足![]() .
.
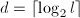 ,
,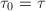 ,
,- 对
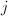 从
从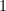 循环到
循环到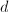 ,执行3~5步,
,执行3~5步, - 计算整数
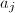 使得
使得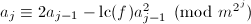 ,
,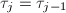 ,将
,将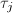 的根结点换为
的根结点换为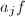 ,
, - 从根结点遍历
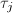 的结点,对每个非叶结点
的结点,对每个非叶结点 ,执行第5步(由根向叶结点方向进行),
,执行第5步(由根向叶结点方向进行), - 调用算法3,输入
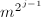 来提升
来提升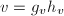 和
和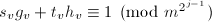 ,提升到模
,提升到模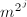 ,
, - 输出
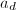 ,
,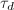 .
.
 应用Hensel提升的Zasenhaus算法
应用Hensel提升的Zasenhaus算法
有了前面的Hensel提升理论,下面我们就可以利用它取代前面的大素数模算法.
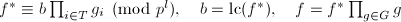 ,
,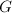 中多项式均不可约,
中多项式均不可约,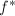 本原且它的任何一个不可约因子
本原且它的任何一个不可约因子![$u\in\mathrm{Z}[x]$](./latex/latex2png-PolyFacZ_16213090_-5.gif) 有
有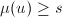 .
.
主要证法和算法1的证明一致,我们只需证明当![]() 有一个不可约因子
有一个不可约因子![]() 满足
满足![]() 时,当循环到s时必然能将此因子选出,这一点可以构造来证明,即取指标集
时,当循环到s时必然能将此因子选出,这一点可以构造来证明,即取指标集![]() 为
为![]() 在
在![]() 中不可约因子的编号.当然这里与前面的证法有所不同,因为
中不可约因子的编号.当然这里与前面的证法有所不同,因为![]() 并不是UFD,要证明唯一性还需要用Hensel提升的唯一性定理.首先可设
并不是UFD,要证明唯一性还需要用Hensel提升的唯一性定理.首先可设![]() ,
,![]() ,再设
,再设![]() ,
,![]() .由
.由![]() 可知
可知
![]() 另外
另外
![]() 以上两式均是
以上两式均是![]() 的提升,于是
的提升,于是![]() 且
且![]() ,再由所定的Mignotte界和
,再由所定的Mignotte界和![]() 的选择可知9中的条件必然成立.
□
的选择可知9中的条件必然成立.
□
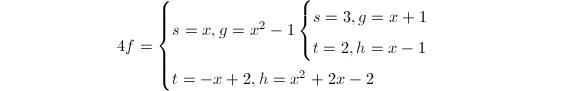
利用多因子提升算法提升为模25因子树:
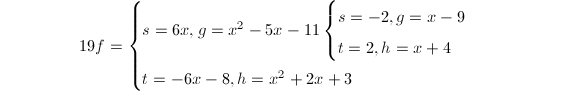 以此类推有模
以此类推有模![]() 因子树:
因子树:
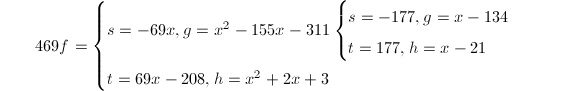 模
模![]() 因子树:
因子树:
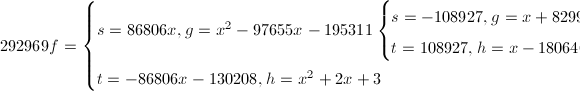 于是我们有
于是我们有![]() .这里我们再对其进行还原时,显然有
.这里我们再对其进行还原时,显然有![]() 时可得到不可约因子
时可得到不可约因子![]() ,此时
,此时![]() .于是再一次得到分解
.于是再一次得到分解![]() .
.
 格中短向量(Short vectors in lattices)理论
格中短向量(Short vectors in lattices)理论
 问题的引入
问题的引入
通过大素数模方法或Hensel提升方法,我们都可以得到多项式![]() 在模某个整数
在模某个整数![]() 后的分解,即
后的分解,即![]() .这时候我们用因子组合的算法将它们拼起来还原.但是这种方法的效率有时候不会很高,如Swinnerton-Dyer多项式(见[1]15.3节).于是我们要发展一套更有效的方法,下面几节将要介绍的格中短向量方法是一种多项式时间算法.
.这时候我们用因子组合的算法将它们拼起来还原.但是这种方法的效率有时候不会很高,如Swinnerton-Dyer多项式(见[1]15.3节).于是我们要发展一套更有效的方法,下面几节将要介绍的格中短向量方法是一种多项式时间算法.
由定义13,以下我们取默认的范数![]() 为2-范数,即
为2-范数,即![]() .我们将多项式的系数看作向量,则多项式范数等同于该向量的范数.
.我们将多项式的系数看作向量,则多项式范数等同于该向量的范数.
由前面我们已得出的分解结果和上面的引理,我们可以设想这样一种分解的想法。首先我们已经有待分解的![]() 次多项式
次多项式![]() 和
和![]() 在模
在模![]() 下的一个因子
下的一个因子![]() ,此时我们需要找到一个较“短”的
,此时我们需要找到一个较“短”的![]() 次多项式
次多项式![]() 使得
使得![]() ,且
,且![]() ,于是可通过
,于是可通过![]() 得到
得到![]() 的一个非平凡因子.为了叙述方便,以后记号
的一个非平凡因子.为了叙述方便,以后记号![]() 既可以表示
既可以表示![]() 次多项式,也可以表示
次多项式,也可以表示![]() 维系数向量.引入下面的定义:
维系数向量.引入下面的定义:
现在我们考虑寻找一个次数小于![]() 的多项式
的多项式![]() ,设
,设![]() 是由
是由![]() 和
和![]() 生成的,即
生成的,即![]() 其中
其中![]() ,这时我们有下面的定理:
,这时我们有下面的定理:
现在我们的问题化为在![]() 中寻找一种约化的基,以使得基向量长度较短,满足要求.
中寻找一种约化的基,以使得基向量长度较短,满足要求.
 约化基算法
约化基算法
下面要介绍的约化基算法即是所谓的3-L算法(Lenstra,Lenstra and Lovász).
若![]() ,则有
,则有![]() -模的范数与生成元无关.由Hadamard不等式我们知道
-模的范数与生成元无关.由Hadamard不等式我们知道![]() .
.
因为范数与基的选择无关,因而我们想到,如果选取的基越“正交”,那么某种程度上这组基矢的长度越短.因而,向量基的正交化可以启示我们得到一种求约化基(即所谓的短矢量)的方法.
现在我们已知由![]() 生成的
生成的![]() -模,即一个
-模,即一个![]() 维格子,若取内积为
维格子,若取内积为![]() ,由高等代数学(见[2]P281)的内容我们知道可以对它们进行Gram-Schmidt正交化,正交化的过程可以归纳地进行,即令
,由高等代数学(见[2]P281)的内容我们知道可以对它们进行Gram-Schmidt正交化,正交化的过程可以归纳地进行,即令![]() ,对于
,对于![]() ,有
,有
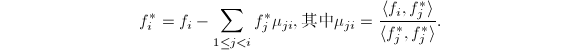 于是存在一个上三角阵
于是存在一个上三角阵![]() ,其对角元为1,使得
,其对角元为1,使得
![]() 其中
其中![]() 张成同样的空间,且两两互相正交.由正交化的几何意义我们可以很明显地看到,每个向量的长度都不大于原向量的长度,即基向量的长度缩短了.但是光作GSO(Gram-Schmidt orthogonalization)是不行的,因为正交化后所得的向量并不一定是原先格子中的向量,这是模和线性空间的不同.但是首先,我们有下面的估计:
张成同样的空间,且两两互相正交.由正交化的几何意义我们可以很明显地看到,每个向量的长度都不大于原向量的长度,即基向量的长度缩短了.但是光作GSO(Gram-Schmidt orthogonalization)是不行的,因为正交化后所得的向量并不一定是原先格子中的向量,这是模和线性空间的不同.但是首先,我们有下面的估计:
于是![]() ,其中
,其中![]() ,将此式代入
,将此式代入![]() 可得:
可得:
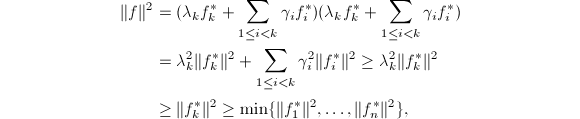 证毕.
□
证毕.
□
既然我们用GSO得到的不一定是格的约化基,那么我们可以放宽条件,下面给出一种约化基的定义方式:
下面给出生成约化基的算法:
输入:线性无关的向量![]() ,
,
输出:由输入向量所生成的![]() -模的约化基
-模的约化基![]() .
.
- 将
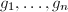 初始化为
初始化为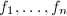 ,并进行相应的GSO过程,得到约化基
,并进行相应的GSO过程,得到约化基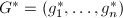 和变换矩阵
和变换矩阵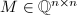 使得
使得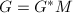 ,
,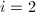 ,
, - 当
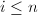 时,执行下面3~5步,
时,执行下面3~5步, - 让
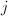 从
从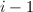 循环到
循环到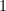 ,执行下面4步,
,执行下面4步, 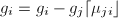 (此处取最接近
(此处取最接近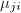 的整数),重新计算GSO得到
的整数),重新计算GSO得到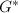 ,
, ,
,- 若
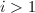 且
且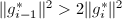 则交换
则交换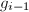 和
和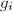 ,并重新计算GSO得到
,并重新计算GSO得到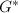 ,
, ,
,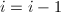 ,否则
,否则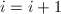 ,
, - 输出
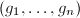 .
.
我们取![]() 作为短矢量,有
作为短矢量,有![]()
如果我们再考虑由![]() 生成的
生成的![]() -模,则按照算法可得如下约化基:
-模,则按照算法可得如下约化基:![]()
![]()
![]() 其中
其中
![]()
此时得到短矢量![]() .
.
 约化基算法的一些细节说明
约化基算法的一些细节说明
对于约化基算法6,它应该是一种说明性质的,实际使用它时有些效率上的不足.例如仔细分析一下我们会发现该算法第4步中的GSO更新是不必要的,可以将这一步省去.而且在每一步交换两个基向量时对GSO的更新也是有很多冗余计算的.当我们采用本节介绍的算法后,我们可以发现它甚至能比原算法效率提高一百倍.
事实上,关于格的约化基的定义方式在各文献中不一致,上节所提的定义方式是文献[1]给出的.A. K. Lenstra, H. W. Lenstra和L. Lovász的文献[3]中就给出了如下定义:
从定义中我们明显看出,本节定义的约化基一定是上一节定义的约化基,其条件更强,因此对后面的算法是没有影响的.下面我们给出新的约化基算法,它在细节处理比前节的算法要节省很多计算.
- 初始化工作.首先将各
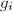 初化为
初化为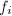 ,并且
,并且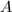 顺次由1循环到
顺次由1循环到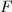 ,做如下步骤2至4,
,做如下步骤2至4, 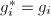 ,
,- 将
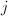 顺次由1循环到
顺次由1循环到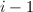 ,计算
,计算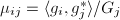 ,
,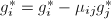 ,
, 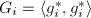 ,
,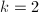 ,并循环做下面6-10步,
,并循环做下面6-10步,- 将
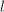 顺次由
顺次由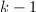 递减到
递减到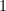 ,做如下7-8步,
,做如下7-8步, - 若
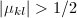 ,则
,则
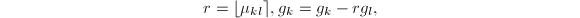 对
对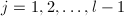 顺次计算
顺次计算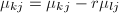 ,并且
,并且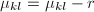 ,
, - 若
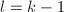 则检验
则检验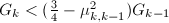 是否成立,若成立则交换
是否成立,若成立则交换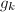 与
与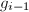 并更新此时的各GSO结果,并直接转第6步,
并更新此时的各GSO结果,并直接转第6步, - 若
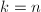 则终止算法并输出
则终止算法并输出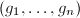 ,
, 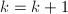 .
.
算法的终止性见[3].
本算法仅在初始化时需要计算诸![]() ,在后面的算法中实际上已不需要它们,只要保存
,在后面的算法中实际上已不需要它们,只要保存![]() 矩阵以及各
矩阵以及各![]() 的模
的模![]() 即可.在本节的开始,我们也提到了在交换两个基矢时对整个GSO的更新实际上包含了很多不必要的计算,因此本算法第8步所提的到的更新GSO步骤是很重要的,我们在下面给出:
即可.在本节的开始,我们也提到了在交换两个基矢时对整个GSO的更新实际上包含了很多不必要的计算,因此本算法第8步所提的到的更新GSO步骤是很重要的,我们在下面给出:
关于更新算法的正确性,只需作一些计算即可证明,这里也不验证了,可以参考[3]P520.
 应用格中短向量的分解算法
应用格中短向量的分解算法
下面以Hensel提升和格中短向量方法为例来说明后者.这里我们先证明一个引理,便于后面算法正确性的证明.
输入:一个无平方因子本原![]() 次多项式
次多项式![]() ,
,![]() 且
且![]() ,
,
输出:![]() 的不可约因子
的不可约因子![]() .
.
- 若
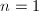 则输出
则输出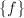 ,否则
,否则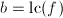 ,
,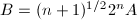 ,
,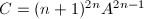 ,
,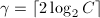 ,
, - 任选素数
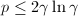 ,
,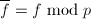 ,直至
,直至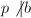 且
且![$\gcd(\overline{f},\overline{f}')=1\in\field{p}[x]$](./latex/latex2png-PolyFacZ_16859241_-5.gif) ,再令
,再令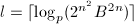 ,
, - 在
![$\field{p}[x]$](./latex/latex2png-PolyFacZ_223283783_-5.gif) 上得到分解
上得到分解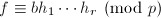 ,各因子无穷范数小于
,各因子无穷范数小于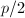 且首一,
且首一, - 利用Hensel提升得到分解
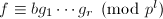 ,各因子不可约且无穷范数小于
,各因子不可约且无穷范数小于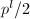 ,首一,
,首一, 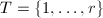 ,
,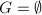 ,
,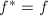 ,
,- 当
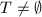 时,做下面7~10步,
时,做下面7~10步, - 在
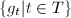 中选择次数最大的因子
中选择次数最大的因子 ,
,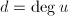 ,
,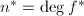 ,对
,对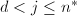 的
的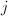 循环做下面8、9步,
循环做下面8、9步, - 调用算法6计算一个短矢量
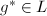 ,其中
,其中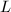 为
为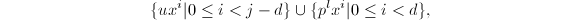
- 用试除法得到
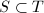 ,其中
,其中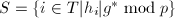 ,计算
,计算![$h^*\in\mathbb{Z}[x]$](./latex/latex2png-PolyFacZ_74668388_-5.gif) 使得其无穷范数小于
使得其无穷范数小于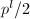 且满足
且满足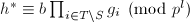 ,若
,若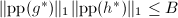 则
则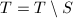 ,
,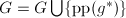 ,
,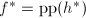 ,
,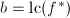 ,转第6步,
,转第6步, 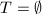 ,
,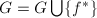 ,
,- 输出
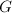 .
.
假设![]() ,令
,令![]() .则
.则![]() .于是
.于是![]() .再由
.再由![]() 的选择,我们有
的选择,我们有![]() 于是由引理3知
于是由引理3知![]() 非平凡,由
非平凡,由![]() 不可约以及
不可约以及![]() 得
得![]() .
.
令![]() ,则由Hensel提升唯一性知在第9步有
,则由Hensel提升唯一性知在第9步有![]() .再由
.再由![]() 大于
大于![]() 的Mignotte界bB,于是
的Mignotte界bB,于是![]() ,且
,且![]() ,算法会到到
,算法会到到![]() 的不可约因子
的不可约因子![]() .
□
.
□
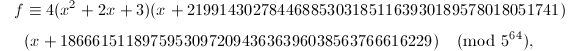 另外由前面例3结果我们知道
另外由前面例3结果我们知道首先![]() ,
,![]() ,则
,则![]() 的生成元为
的生成元为![]() 很显然
很显然![]() 应该是一个短向量,由试除法得到
应该是一个短向量,由试除法得到![]() ,
,![]() ,显然满足条件,得到一个不可约因子
,显然满足条件,得到一个不可约因子![]() ,此时
,此时![]() ,
,![]() .此时我们再取因子
.此时我们再取因子![]()
![]() ,
,![]() ,
,![]() 只能取
只能取![]() ,则得到
,则得到![]() 的生成元
的生成元![]() ,由例4得到
,由例4得到![]()
![]() 是本原的且是
是本原的且是![]() ,由试除法知
,由试除法知![]() ,但此时已有
,但此时已有![]() ,故此时无解,循环结束,第二个不可约因子为此时的
,故此时无解,循环结束,第二个不可约因子为此时的![]() .
.
其实我们第一步如果不取最大次数的![]() ,可以对短向量方法有更深的体会.若取
,可以对短向量方法有更深的体会.若取![]() ,当
,当![]() 时则由例4后面的讨论可知此时得到短向量
时则由例4后面的讨论可知此时得到短向量![]() .
.
参考文献
[1]Modern Computer Algebra, Cambridge University Press, 2002.
[2]高等代数学, 清华大学出版社, 北京, 2004.
[3]Factoring Polynomials with Rational Coefficients, Mathematicsche Annaln (1982), no.261, 515-534.