本章主要讨论超定方程组与不定方程组的最小二乘解,即![]() 的最小化,其中
的最小化,其中![]() .解此问题的可靠方法是通过正交变换将
.解此问题的可靠方法是通过正交变换将![]() 约化为各种典型形式.我们在以下的讨论中主要考虑实矩阵.但容易看出,复矩阵的
约化为各种典型形式.我们在以下的讨论中主要考虑实矩阵.但容易看出,复矩阵的![]() 分解完全可以仿照实矩阵进行.
分解完全可以仿照实矩阵进行.
 Householder反射
Householder反射
通过正交变换将矩阵约化为典型形式 (如Hessenberg形式)的典型方法是通过一系列正交变换,逐个地将矩阵列向量的某些指定分量化为![]() .下面我们就先讨论这一过程的两种实现:Householder反射与Jacobi-Givens旋转.
.下面我们就先讨论这一过程的两种实现:Householder反射与Jacobi-Givens旋转.
Householder反射的几何意义是取向量![]() 关于指定超平面
关于指定超平面![]() 的反射.
的反射.![]() 为向量
为向量![]() 关于平面
关于平面![]() 的法线的投影,从而
的法线的投影,从而![]() 为
为![]() 关于该平面的投影.因此,设
关于该平面的投影.因此,设![]() 是非零向量,称形如
是非零向量,称形如![]() 的
的![]() 矩阵
矩阵![]() 为Householder反射.如果用
为Householder反射.如果用![]() 去乘向量
去乘向量![]() ,则得到
,则得到![]() 是
是![]() 关于超平面
关于超平面![]() 的反射.
的反射.
利用Householder反射可将一个向量的某些选定分量变为![]() .设给定
.设给定![]() ,欲使
,欲使![]() 沿
沿![]() 的方向.由几何直观容易知道
的方向.由几何直观容易知道
![]() 有一些细节需要注意:
有一些细节需要注意:
- 由于
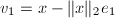 使得
使得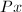 是
是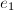 的正倍数,故常常采用.但当
的正倍数,故常常采用.但当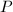 接近
接近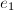 的一个正倍数时,则会出现严重的相消.由
的一个正倍数时,则会出现严重的相消.由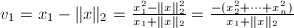 在
在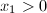 的情况下则可避免相消.
的情况下则可避免相消. - 实际中常常将Householder向量规范化使得
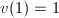 ,这就允许将
,这就允许将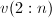 存储到
存储到 已化零的位置,即
已化零的位置,即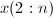 ,而无需增加额外的存储开销.在这种情况下,我们将
,而无需增加额外的存储开销.在这种情况下,我们将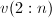 称为Householder向量的基本部分.
称为Householder向量的基本部分. - 在进行Householder矩阵与向量的乘法运算时,我们并不直接采用矩阵-向量乘法,而是采用
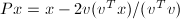 的运算顺序,可以显著减少运算量.
的运算顺序,可以显著减少运算量. - 在基于Householder反射的矩阵分解算法中,常用到形如
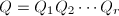 ,
,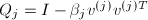 的若干个Householder矩阵的乘积,其中
的若干个Householder矩阵的乘积,其中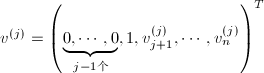 .通常我们并不显式地求出
.通常我们并不显式地求出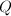 ,而是将其保持因子形式,逐个作用到给定矩阵上去,在不需显式求出变换矩阵时可显著减少运算量.
,而是将其保持因子形式,逐个作用到给定矩阵上去,在不需显式求出变换矩阵时可显著减少运算量. - 若要将
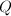 显式求出(或部分求出),则采用向后累积的形式,即先将
显式求出(或部分求出),则采用向后累积的形式,即先将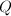 赋值为单位矩阵,依次计算
赋值为单位矩阵,依次计算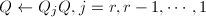 .这样可以减少运算所需的flop数.
.这样可以减少运算所需的flop数.
 Jacobi-Givens旋转
Jacobi-Givens旋转
Jacobi-Givens旋转是指在特定二维坐标坐标平面内进行的旋转,其一般形式为
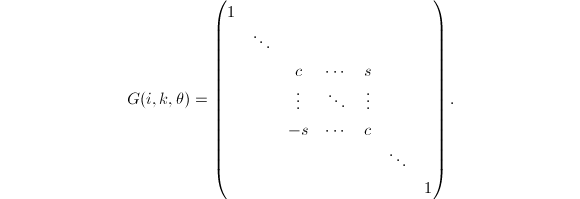 其中
其中![]() ,
,![]() ,
,![]() 和
和![]() 等分别位于第
等分别位于第![]() 行和第
行和第![]() 行.
行.
用![]() 左乘即产生在
左乘即产生在![]() 坐标平面的
坐标平面的![]() 角的旋转.运用Givens旋转可有选择地消去一些矩阵元素.
角的旋转.运用Givens旋转可有选择地消去一些矩阵元素.
若![]() ,
,![]() ,则
,则
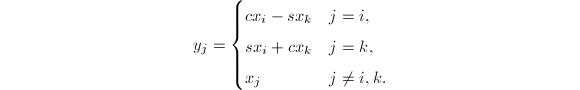 若令
若令
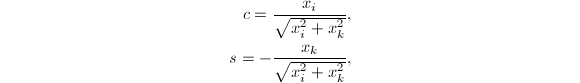 则可将
则可将![]() 化为
化为![]() .通过合理运算顺序安排,可以避免计算中溢出发生.本算法共需
.通过合理运算顺序安排,可以避免计算中溢出发生.本算法共需![]() 个flop和
个flop和![]() 次平方根运算.
次平方根运算.
在应用Givens旋转时,同样有一些细节问题需要特别注意:
- 当用Givens矩阵进行左乘或右乘修正时,应注意到它只影响矩阵的两行或两列.
- 同Householder变换类似,多个Givens矩阵的乘积通常并不显式地出现.
- 可将每一个旋转变换对应于一个浮点数
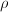 ,从而将其存储在向量已消元的位置,通常在正弦较小时存储
,从而将其存储在向量已消元的位置,通常在正弦较小时存储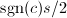 ,余弦较小时存储
,余弦较小时存储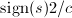 .可以由
.可以由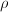 重新构造Givens矩阵.
重新构造Givens矩阵.
除标准Givens变换外,还有所谓快速Givens变换,又称"免平方根 (square root-free) Givens变换".将在应用时介绍.

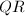 分解
分解
一个![]() 矩阵
矩阵![]() 的
的![]() 分解为
分解为![]() ,其中
,其中![]() 是正交矩阵,
是正交矩阵,![]() 是上三角矩阵.本节将讨论
是上三角矩阵.本节将讨论![]() 且
且![]() 为列满秩情形下的
为列满秩情形下的![]() 分解,主要工具为Householder变换,Givens变换以及Gram-Schmidt正交化方法.
分解,主要工具为Householder变换,Givens变换以及Gram-Schmidt正交化方法.
 Householder
Householder 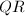 分解
分解
利用Householder变换进行![]() 分解是直截了当的,可给出算法描述如下:
分解是直截了当的,可给出算法描述如下:
 Givens
Givens  方法
方法
选择一个合适的消去的顺序,Givens ![]() 分解也是简单有效的.如通过自左而右逐列考察,每一列中通过自下而上地进行Givens变换对
分解也是简单有效的.如通过自左而右逐列考察,每一列中通过自下而上地进行Givens变换对![]() 引入零元,共需
引入零元,共需![]() 个flop即可将
个flop即可将![]() 化为上三角形式.Givens变换矩阵累积起来即得到正交变换矩阵
化为上三角形式.Givens变换矩阵累积起来即得到正交变换矩阵![]() .我们也可以将
.我们也可以将![]() 用单个浮点数
用单个浮点数![]() 表示,从而将其存储在已化零的
表示,从而将其存储在已化零的![]() 中.
中.
下面讨论快速Givens ![]() 方法.
方法.
快速Givens方法思想就是当![]() 是一系列Givens旋转的乘积时巧妙地表达它.具体地说,
是一系列Givens旋转的乘积时巧妙地表达它.具体地说,![]() 用一个矩阵对
用一个矩阵对![]() 来表示,其中
来表示,其中![]() 且
且![]() .矩阵
.矩阵![]() ,
,![]() 和
和![]() 通过公式
通过公式![]() 联系起来.易知
联系起来.易知![]() 是正交的.若
是正交的.若![]() 使
使![]() 是对角阵,则取
是对角阵,则取![]() 满足
满足![]() .从而由快速Givens的表示形式
.从而由快速Givens的表示形式![]() 做变换即可得到
做变换即可得到![]() .
.
以![]() 维的情形来说明以上思想.令
维的情形来说明以上思想.令![]() ,给定
,给定![]() .定义
.定义![]() ,则
,则
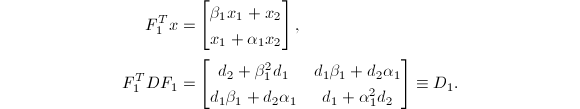 若
若![]() ,取
,取![]() ,
,![]() ,则
,则
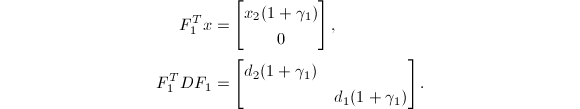 其中
其中![]() .
.
类似地,如果![]() ,则可定义
,则可定义![]() ,其中
,其中![]() .则
.则
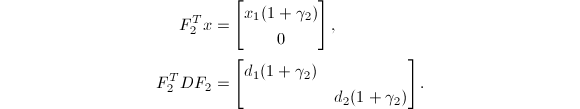 其中
其中![]() .
.
这样,我们就完成了对该算法思想的描述.实际中选择变化类型使矩阵元素的"增长因子"![]() 以
以![]() 为界.
为界.
借助快速Givens变换,我们可以计算非奇异的![]() 和正的
和正的![]() 使得
使得![]() 为上三角阵,且
为上三角阵,且![]() .则
.则![]() 是
是![]() 的
的![]() 分解.这种算法需要
分解.这种算法需要![]() 个flop,且不涉及平方根运算.
个flop,且不涉及平方根运算.
Givens方法对于稀疏矩阵问题,尤其是带状矩阵问题有特别的优势,例如对Hessenberg矩阵进行![]() 分解只需要
分解只需要![]() 个flop.
个flop.
 Gram-Schmidt方法
Gram-Schmidt方法
经典Gram-Schmidt方法(CGS)是我们熟知的,通过对![]() 的各列施行正交化手续,每步求出
的各列施行正交化手续,每步求出![]() 和
和![]() 的一列.但CGS的数值特性非常差,
的一列.但CGS的数值特性非常差,![]() 的正交性经常会严重损失.通过改变计算次序,得到修正Gram-Schmidt方法(MGS),则可靠得多.
的正交性经常会严重损失.通过改变计算次序,得到修正Gram-Schmidt方法(MGS),则可靠得多.
在MGS的第![]() 步,求出
步,求出![]() 的第
的第![]() 列
列![]() 和
和![]() 的第
的第![]() 行
行![]() .定义矩阵
.定义矩阵![]() 为
为
![]() 因此,如果
因此,如果![]() ,则有
,则有
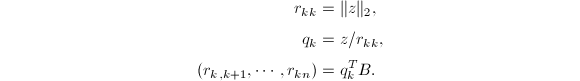 随后计算外积
随后计算外积
![]() 并进行下一步.这样我们就完成了对MGS算法第
并进行下一步.这样我们就完成了对MGS算法第![]() 步的描述.这一算法共需
步的描述.这一算法共需![]() 个flop.但MGS的缺点在于
个flop.但MGS的缺点在于![]() 病态时,不能保证良好的正交性.故仅当在被正交化的向量独立性很强时,才可用MGS求正交基.
病态时,不能保证良好的正交性.故仅当在被正交化的向量独立性很强时,才可用MGS求正交基.
 满秩的最小二乘问题
满秩的最小二乘问题
要求找到向量![]() 使
使![]() ,其中
,其中![]() 和
和![]() .若
.若![]() ,即方程个数多于未知数个数,则称方程组
,即方程个数多于未知数个数,则称方程组![]() 是超定 (overdeterminant) 的,通常这样的方程组没有严格解.在实际中,我们考虑对适当选取的
是超定 (overdeterminant) 的,通常这样的方程组没有严格解.在实际中,我们考虑对适当选取的![]() ,极小化
,极小化![]() .不同的范数给出不同的最优解,其中应用较多的是
.不同的范数给出不同的最优解,其中应用较多的是![]() 的情形.其中,2-范数情形便于解析求解.此时,该问题称为最小二乘(Least Square,LS)问题.
的情形.其中,2-范数情形便于解析求解.此时,该问题称为最小二乘(Least Square,LS)问题.
容易证明,若![]() 是列满秩的,则存在唯一的LS解
是列满秩的,则存在唯一的LS解![]() ,它是对称正定线性方程组
,它是对称正定线性方程组![]() 的解,这一方程组称为法方程组.称
的解,这一方程组称为法方程组.称![]() 为最小剩余,用
为最小剩余,用![]() 表示其大小.
表示其大小.
当评估一个LS解![]() 的质量时,常考虑两方面的问题:
的质量时,常考虑两方面的问题:
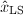 有多靠近
有多靠近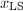 ?
?- 与
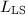 相比,
相比,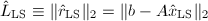 有多小?
有多小?
这两条标准在实际应用中常要考虑.
 法方程组方法
法方程组方法
这一算法基于许多标准算法,共需要
 用
用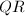 分解求解LS问题
分解求解LS问题
设![]() ,
,![]() 且
且![]() 给定.若以计算得到
给定.若以计算得到![]() 的
的![]() 分解
分解
![\begin{equation*}
Q^TA=R=
\begin{bmatrix}
R_1\\
O
\end{bmatrix}
\begin{array}[c]{l}
\}n\\
\}m-n
\end{array},
\end{equation*}](./latex/latex2png-QRLS_234909637_.gif) 其中
其中![]() 是
是![]() 上三角阵.记
上三角阵.记
![\begin{equation*}
\begin{bmatrix}
c\\
d
\end{bmatrix}
\begin{array}[c]{l}
\}n\\
\}m-n
\end{array}
\end{equation*}](./latex/latex2png-QRLS_28380231_.gif) 则
则
![]() 于是,
于是,![]() 由三角方程组
由三角方程组![]() 定义,且
定义,且![]() .于是,只要求得
.于是,只要求得![]() 的
的![]() 分解,LS问题就很容易了.如采用Householder算法求得
分解,LS问题就很容易了.如采用Householder算法求得![]() 的
的![]() 分解,则求解满秩LS问题,共需
分解,则求解满秩LS问题,共需![]() 个flop.
个flop.
经分析,这种方法在![]() 时失败.事实上,其解的灵敏性大致与
时失败.事实上,其解的灵敏性大致与![]() 成正比.因此,
成正比.因此,![]() 分解的方法适用范围比法方程组方法大一些.
分解的方法适用范围比法方程组方法大一些.
基于MGS以及快速Givens方法的![]() 分解也可用于求解LS问题,且解的稳定性相当.
分解也可用于求解LS问题,且解的稳定性相当.
 病态矩阵的正交分解
病态矩阵的正交分解
如果![]() 是秩亏损的,则
是秩亏损的,则![]() 分解不一定能给出
分解不一定能给出![]() 的一组正交基.这问题可通过计算经过置换后的
的一组正交基.这问题可通过计算经过置换后的![]() 的
的![]() 分解来解决,即
分解来解决,即![]() ,其中
,其中![]() 是置换阵.
是置换阵.
如果右乘一个一般正交阵![]() ,
,![]() 中的数据可被进一步压缩
中的数据可被进一步压缩![]() .
.![]() 和
和![]() 的选取以及相应的列主元的
的选取以及相应的列主元的![]() 分解正是本节要讨论的.
分解正是本节要讨论的.
 选主列的
选主列的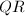 分解
分解
设![]() 且
且![]() ,则
,则![]() 分解不一定产生
分解不一定产生![]() 的一组正交基.但通过简单的修改,即计算分解
的一组正交基.但通过简单的修改,即计算分解
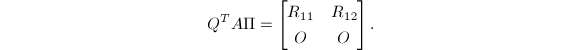 其中
其中![]() 为正交矩阵,
为正交矩阵,![]() 为
为![]() 非奇异的上三角矩阵.于是
非奇异的上三角矩阵.于是![]() 的前
的前![]() 列给出
列给出![]() 的正交基.
的正交基.
![]() 和
和![]() 分别是Householder矩阵和初等置换阵之积.假定对某个
分别是Householder矩阵和初等置换阵之积.假定对某个![]() ,我们已计算了Householder矩阵
,我们已计算了Householder矩阵![]() 和置换阵
和置换阵![]() 使得
使得
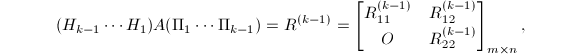 其中
其中![]() 为
为![]() 阶非奇异上三角阵.假定
阶非奇异上三角阵.假定
![]() 且令
且令![]() 为其中2-范数最大者.注意若
为其中2-范数最大者.注意若![]() ,则该最大模是
,则该最大模是![]() ,计算至此结束.否则,令
,计算至此结束.否则,令![]() 是互换第
是互换第![]() 列和第
列和第![]() 列的置换阵,并确定Householder矩阵
列的置换阵,并确定Householder矩阵![]() 使
使![]() 有
有![]() .换句话说,
.换句话说,![]() 把最大列移到前面,
把最大列移到前面,![]() 把它的非对角元化为
把它的非对角元化为![]() .
.
利用对正交阵![]()
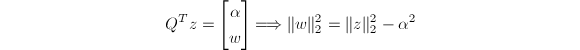 的性质,我们只需修正旧的列范数得到新的列范数,即
的性质,我们只需修正旧的列范数得到新的列范数,即
![]() 从而使选主列的工作量从
从而使选主列的工作量从![]() 减少到
减少到![]() .这样,我们就完成了对该算法的描述.
.这样,我们就完成了对该算法的描述.
本算法共需![]() 个flop,其中
个flop,其中![]() .正交矩阵
.正交矩阵![]() 可以以因子形式存储与
可以以因子形式存储与![]() 的对角线之下.
的对角线之下.
 完全正交分解
完全正交分解
如果对上述算法产生的![]() ,从右边用一组适当的Householder矩阵相乘,则它可以进一步缩小.具体地说,我们可通过列满秩的
,从右边用一组适当的Householder矩阵相乘,则它可以进一步缩小.具体地说,我们可通过列满秩的![]() 分解来计算
分解来计算
![\begin{equation*}
Z_r\cdots Z_1
\begin{bmatrix}
R_{11}^T\\
R_{12}^T
\end{bmatrix}
=
\begin{bmatrix}
T_{11}^T\\
O
\end{bmatrix}
\begin{array}[c]{l}
\}r\\
\}n-r
\end{array}.
\end{equation*}](./latex/latex2png-QRLS_192447912_.gif) 其中,
其中,![]() 为Householder变换,
为Householder变换,![]() 是上三角矩阵,于是有
是上三角矩阵,于是有
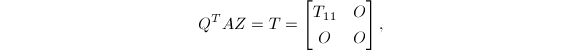 其中,
其中,![]() .我们称其为完全正交分解.在这种情况下,
.我们称其为完全正交分解.在这种情况下,![]() .
.
 双对角化
双对角化
矩阵的双对角化即通过正交变换将矩阵化为上双对角形 (上带宽为一的带状阵).![]() 的双对角化与
的双对角化与![]() 的三对角化密切相关.通过对双对角阵
的三对角化密切相关.通过对双对角阵![]() 的迭代运算,可以得到
的迭代运算,可以得到![]() 的奇异值分解(SVD).我们将其放在"对称特征值问题"一章中讨论.
的奇异值分解(SVD).我们将其放在"对称特征值问题"一章中讨论.
假定![]() 且
且![]() .我们要计算正交阵
.我们要计算正交阵![]() 和
和![]() 使
使
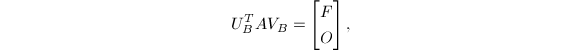 其中,
其中,![]() 为上双对角阵,即上带宽为
为上双对角阵,即上带宽为![]() .很容易通过直接的Householder变换,使
.很容易通过直接的Householder变换,使
![]() 其中,算法进行的第
其中,算法进行的第![]() 步,
步,![]() 将
将![]() 化为
化为![]() ,而
,而![]() 将
将![]() 化为
化为![]() .本算法共需
.本算法共需![]() 个flop.
个flop.
当![]() 时,若在进行双对角化之前先进行上三对角化,则可得到一个更为快速的双对角化算法,称为R双对角化.具体地说,假定我们计算一个正交阵
时,若在进行双对角化之前先进行上三对角化,则可得到一个更为快速的双对角化算法,称为R双对角化.具体地说,假定我们计算一个正交阵![]() 使得
使得
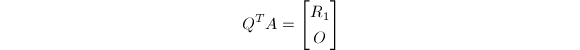 是上三角阵.然后对
是上三角阵.然后对![]() 进行双对角化
进行双对角化
![]() 则
则
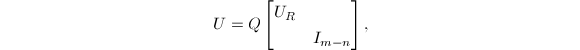 而
而
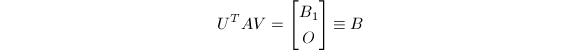 是
是![]() 的双对角化.它需要
的双对角化.它需要![]() 个flop.可以看出,
个flop.可以看出,![]() 时,它的计算量要少一些.
时,它的计算量要少一些.
 秩亏损的LS问题
秩亏损的LS问题
当![]() 是秩亏损的,则LS问题就有无穷多个解.可以证明,所有极小解的集合:
是秩亏损的,则LS问题就有无穷多个解.可以证明,所有极小解的集合:![]() 是凸集,从而存在唯一元素具有极小2-范数,记为
是凸集,从而存在唯一元素具有极小2-范数,记为![]() .
.
 完全正交分解,SVD与
完全正交分解,SVD与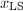
任何完全正交分解都可用来计算![]() .设
.设
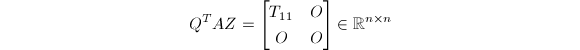 为
为![]() 的完全正交分解,其中
的完全正交分解,其中![]() 为
为![]() 上三角矩阵,
上三角矩阵,![]() 为
为![]() 的秩.则
的秩.则
![]() 其中
其中
![\begin{align*}
Z^Tb&=
\begin{bmatrix}
w\\
y
\end{bmatrix}
\begin{array}[c]{l}
\}r\\
\}n-r
\end{array},\\
Q^Tb&=
\begin{bmatrix}
c\\
d
\end{bmatrix}
\begin{array}[c]{l}
\}r\\
\}m-r
\end{array}.
\end{align*}](./latex/latex2png-QRLS_53657522_.gif) 于是
于是
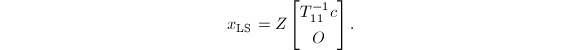
SVD是非常"显露"的完全正交分解,当然可以用它来计算![]() ,并有以下定理,它提供了
,并有以下定理,它提供了![]() 的一个简洁表达式和最小剩余量的范数
的一个简洁表达式和最小剩余量的范数![]() .
.
设
![]() 是
是![]() 的SVD,则
的SVD,则![]() 的广义逆(又称Moore-Penrose广义逆或加号广义逆)
的广义逆(又称Moore-Penrose广义逆或加号广义逆)![]() 为
为
![]() 其中
其中
![]() 则
则
![]() 且
且
![]()
![]() 是
是![]() 的唯一的最小Frobenius范数解.
的唯一的最小Frobenius范数解.
LS问题在![]() 秩亏损时变得相当困难,
秩亏损时变得相当困难,![]() 甚至不是
甚至不是![]() 中元素的的连续函数.
中元素的的连续函数.![]() 和
和![]() 的微小变化可能引起
的微小变化可能引起![]() 的任意大的变化.
的任意大的变化.
 选主列的
选主列的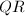 分解与基本解
分解与基本解
假定![]() 秩为
秩为![]() ,选主列的
,选主列的![]() 分解给出
分解给出
![]() 其中
其中
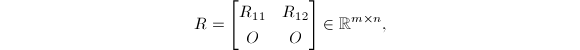
![]() 为
为![]() 满秩上三角阵.则对任意
满秩上三角阵.则对任意![]() 有
有
![]() 其中
其中
![\begin{align*}
\Pi^Tx=
\begin{bmatrix}
y\\
z
\end{bmatrix}
\begin{array}[c]{l}
\}r\\
\}n-r
\end{array},\\
Q^Tb=
\begin{bmatrix}
c\\
d
\end{bmatrix}
\begin{array}[c]{l}
\}r\\
\}m-r
\end{array}.
\end{align*}](./latex/latex2png-QRLS_192873843_.gif) 于是,若
于是,若![]() 是一个极小解,则有
是一个极小解,则有
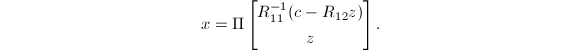 若取
若取![]() ,则得到所谓基本解
,则得到所谓基本解
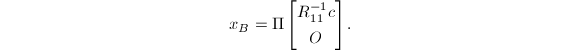 可以看到,
可以看到,![]() 至多只有
至多只有![]() 个非零分量.但除非
个非零分量.但除非![]() ,基本解一般不是最小2-范数解.
,基本解一般不是最小2-范数解.
 欠定方程组的LS解
欠定方程组的LS解
当![]() 时,我们称线性方程组
时,我们称线性方程组![]() 是欠定的(underdetermined),它要么无解,要么有无穷多解.我们希望求出它的最小2-范数解.以下我们先讨论系数矩阵
是欠定的(underdetermined),它要么无解,要么有无穷多解.我们希望求出它的最小2-范数解.以下我们先讨论系数矩阵![]() 行满秩情形的算法,随后对秩亏损(但非矛盾)的情形加以考察.本节的讨论主要来自[1].
行满秩情形的算法,随后对秩亏损(但非矛盾)的情形加以考察.本节的讨论主要来自[1].
 广义逆
广义逆
设欠定方程组![]() ,其中
,其中![]() 为行满秩的系数矩阵.于是
为行满秩的系数矩阵.于是![]() 矩阵
矩阵![]() 非奇异,且
非奇异,且![]() 正是方程组的最小2-范数解,其中
正是方程组的最小2-范数解,其中![]() 是
是![]() 的Moore-Penrose广义逆
的Moore-Penrose广义逆![]() .
.
一个直接的算法是显式形成![]() ,用Cholesky分解或
,用Cholesky分解或![]() 分解求解得到
分解求解得到![]() .但误差理论指出,若显式计算
.但误差理论指出,若显式计算![]() ,因条件数增大 (
,因条件数增大 (![]() ) 可能会造成精度的严重丢失.因而这种方法并不可取.
) 可能会造成精度的严重丢失.因而这种方法并不可取.

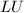 分解
分解
- 计算
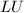 分解
分解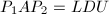 .
. - 由向前消去法求下三角方程
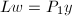 的解.
的解. - 计算
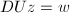 的最小2-范数解,其详细做法将随后叙述.
的最小2-范数解,其详细做法将随后叙述. - 取
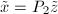 ,即要求的最小2-范数解.
,即要求的最小2-范数解.
在计算![]() 分解时,只借助行选主元也能保证计算的稳定性,同时能够大大减少比较的次数.
分解时,只借助行选主元也能保证计算的稳定性,同时能够大大减少比较的次数.
![]() 的计算可以通过显式形成
的计算可以通过显式形成![]() 来进行,因
来进行,因![]() 是单位上梯形阵,其条件数会小于
是单位上梯形阵,其条件数会小于![]() .以下还会介绍其他的方法.
.以下还会介绍其他的方法.
 正交分解法
正交分解法
通过运用Householder变换或MGS对系数矩阵![]() 进行选主元的
进行选主元的![]() 分解 (即
分解 (即![]() 分解的列形式,其中
分解的列形式,其中![]() 是正交列),得到
是正交列),得到
![]() 其中
其中![]() 为
为![]() 单位下三角阵,
单位下三角阵,![]() 为
为![]() 的矩阵满足
的矩阵满足![]() 为非奇异的对角阵.则最小2-范数解
为非奇异的对角阵.则最小2-范数解
![]() 其中
其中![]() 满足
满足![]() .
.
 消去法
消去法
最小二乘解![]() 也可通过如下的正交分解过程得到.
也可通过如下的正交分解过程得到.
 消去与投影法
消去与投影法
我们考虑一个直接构造欠定方程组的最小2-范数解的方法.注意到方程组的所有解的![]() 都可表为
都可表为
![]() 其中
其中![]() ,
,![]() 且
且![]() 与
与![]() 互为正交补.故
互为正交补.故
![]() 从而
从而
![]() 是
是![]() 到
到![]() 的正交投影.于是我们采用下述步骤就可得到
的正交投影.于是我们采用下述步骤就可得到![]() :
:
- 求出方程组的任意非零解
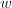 .
. - 求得
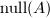 的一组正交基
的一组正交基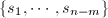 .记
.记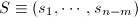 .
. - 做正交投影
![\begin{equation*}
\tilde{x}=\left[I-S (S^T S)^{-1}S^T\right]w.
\end{equation*}](./latex/latex2png-QRLS_125087290_.gif)
下面具体说明:
- 做
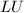 分解
分解
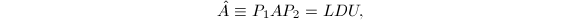 记
记![$U= [U_1,U_2]$](./latex/latex2png-QRLS_31467133_-5.gif) ,其中
,其中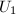 为
为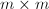 上三角阵.令
上三角阵.令
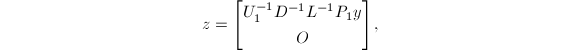 则
则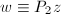 为方程组的一个解,
为方程组的一个解,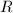 可通过两次消去法得到.
可通过两次消去法得到. - 由于
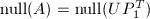 ,故向量
,故向量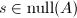 当且仅当
当且仅当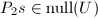 .于是我们只要计算
.于是我们只要计算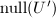 的一组正交基.首先注意到通过对
的一组正交基.首先注意到通过对
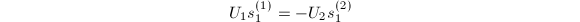 实施向后消去法,即可得到
实施向后消去法,即可得到
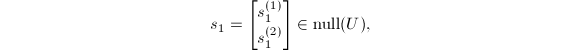 其中
其中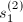 为任意取定的
为任意取定的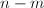 维非零向量.得到
维非零向量.得到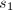 后,通过(非选主元的)Gauss消去法将
后,通过(非选主元的)Gauss消去法将
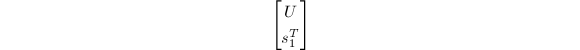 化为上梯形阵(实际只要对最后一行实施初等变换)
化为上梯形阵(实际只要对最后一行实施初等变换)
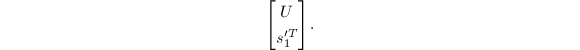 而后求得
而后求得
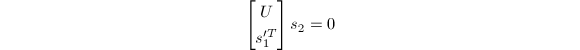 的解
的解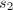 .类似可依次由
.类似可依次由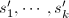 得到
得到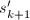 .在此过程中一般地要进行后
.在此过程中一般地要进行后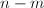 列的交换
列的交换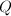 .记
.记
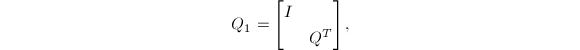 则
则
![\begin{gather*}
\mathrm{null} (U')=\mathrm{span} (Q_1S),\\
\tilde{x}=P_2Q_1\left[I-S (S^T S)^{-1}S^T\right]z.
\end{gather*}](./latex/latex2png-QRLS_31259872_.gif)
- 计算
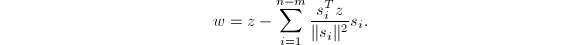 令
令
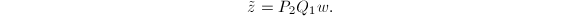
 秩亏损情形
秩亏损情形
在![]() 为行不满秩且方程组不矛盾时,我们称之为秩亏损情形.设
为行不满秩且方程组不矛盾时,我们称之为秩亏损情形.设![]() 为
为![]() 秩的
秩的![]() 矩阵,且有分解
矩阵,且有分解
![]() 其中
其中![]() 为
为![]() 单位下梯形阵,
单位下梯形阵,![]() 为
为![]() 对角阵,
对角阵,![]() 为
为![]() 单位上梯形阵.记
单位上梯形阵.记
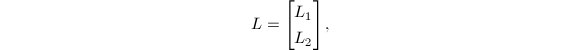 其中
其中![]() 为
为![]() 下三角阵,则
下三角阵,则![]() 可化为等价的
可化为等价的
![]() 其中
其中![]() 可通过向后消去法求解
可通过向后消去法求解
![]() 得到
得到
![]() 其中
其中![]() 表示
表示![]() 的前
的前![]() 维分量.这样原方程组就化为
维分量.这样原方程组就化为
![]() 可通过之前的方法求解.
可通过之前的方法求解.
综合考虑算法的稳定性与复杂度,一般认为基于Householder变换的正交分解法较好,而投影方法在![]() 略小于
略小于![]() 时较为快速.
时较为快速.
 广义最小二乘问题
广义最小二乘问题
若已知![]() ,
,![]() ,
,![]() ,要求
,要求![]() 使
使
![]() 其中
其中![]() ,这一类问题通常称为广义最小二乘问题.Paige (1979)[2]在假定
,这一类问题通常称为广义最小二乘问题.Paige (1979)[2]在假定![]() ,
,![]() 为满秩的情况下,提出了如下算法:
为满秩的情况下,提出了如下算法:
参考文献
[1]L2-Solution to Underdetermined Linear Systems, SIAM Review 18 (1976), 92-106.
[2]Computer Solution and Perturbation Analysis of Generalized Least Squares Problems, Math. Comp. 33 (1979), 171-184.
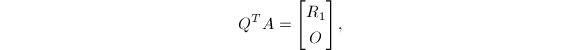 其中,
其中,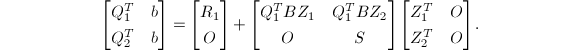 方程下半部分可解出
方程下半部分可解出