一元多项式求值和插值

求值算法
插值算法

求值算法

提起求值算法,我们都会想起最著名的Horner规则,即对于 $f(x)=\sum_{0\le i<n}f_ix^i$ ,利用下式来求其值: $f(x)=(\cdots(f_{n-1}x+f_{n-2})x+\cdots+f_1)x+f_0.$ 在该算法中,需要计算总共 $2n-2$ 次乘法和加法.如果要同时计算 $n$ 个不同点处多项式的值,则需要 $O(n^2)$ 的计算.

下面给出一种快速求值算法,其计算复杂度为 $M(n)\log n$ ,其中 $M(n)$ 为 $n$ 次多项式乘法计算的复杂度(见[1]).为了说明算法,我们取 $n=2^k$ 是2的一整数次幂,需要求值的点为 $u_0,u_1,\ldots,u_{n-1}$ ,并且令 $m_j=x-u_j(j=0,\ldots,n-1)$ .下面构造一棵完全二叉树,以 $M_{i,j}$ 表示从叶( $i=0$ )往上数第 $i$ 层,从该层左往右数第 $j$ 个结点,并且 $M_{i,j}=\prod_{j\cdot 2^i\le l<(j+1)\cdot 2^i}m_l,$ 下图表示其结构:

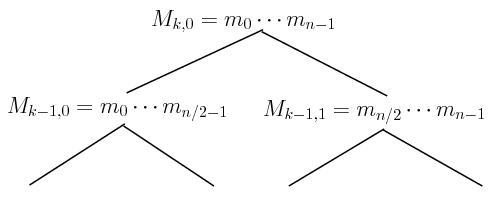$$M_{i,j}$二叉树示意图$

$M_{i,j}$二叉树示意图

其中每个叶结点都是一次式 $M_{0,j}=m_j$ .下面的算法给出了上面树的构造算法:

算法1( $M_{i,j}$ 二叉树构造算法)

对 $0\le j<n$ ,令 $M_{0,j}=m_j$ ,
对 $i$ 从 $1$ 循环到 $k$ ,做下面第3步,
对 $j$ 从 $0$ 循环到 $2^{k-i}$ , $M_{i,j}=M_{i-1,2j}M_{i-1,2j+1}$ .

利用上面的构造的二叉树,我们可以实现快速求值算法.

算法2(快速求值算法)

输入:多项式 $f$ 和 $n(\deg f<n)$ 个点 $u_0,\ldots,u_{n-1}$ ,

输出: $f(u_0),\ldots,f(u_{n-1})$ .

若 $n=1$ 则输出 $f$ ,
$r_0=f\bmod M_{k-1,0}$ , $r_1=f\bmod M_{k-1,1}$ ,
递归调用本算法求 $r_0(u_0),\ldots,r_0(u_{n/2-1})$ ,
递归调用本算法求 $r_1(u_{n/2}),\ldots,r_1(u_{n-1})$ ,
输出上面两步求出的 $n$ 个值.

插值算法

首先我们想到了著名的拉格朗日插值(Lagrange interpolation)算法,设已知 $n$ 个点 $u_0,\ldots,u_{n-1}$ 和多项式在这些点上的值 $v_0,\ldots,v_{n-1}$ ,如果我们引入下面一些记号: $m_j=x-u_j$ , $m=\prod_{0\le j<n}m_j$ , $s_i=\prod_{j\neq i,0\le j<n}\displaystyle\frac{1}{u_i-u_j}$ ,则Lagrange插值的结果可以表示为: $f=\sum_{0\le i<n}\frac{v_is_im}{m_i}.$ 这是一个复杂度 $O(n^2)$ 的算法.

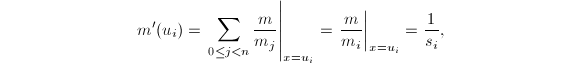下面提出的快速插值算法,其复杂度也为 $M(n)\log n$ .我们考虑问题的核心是要求上面的插值,首先我们要求出 $s_i$ ,因为 $m'(u_i)=\left.\sum_{0\le j<n}\frac{m}{m_j}\right|_{x=u_i}=\left.\frac{m}{m_i}\right|_{x=u_i}=\frac{1}{s_i},$ 故 $s_i=\displaystyle\frac{1}{m'(u_i)}$ .现在令 $c_i=v_is_i$ ,并设 $n=2^k$ 是2的整数次幂.