以前所讨论的是适用于一般矩阵计算的直接法,它们适合求解一般的稠密矩阵问题.本章将讨论特别适用于大规模稀疏矩阵特定问题求解的迭代法.
 概述
概述
以后所介绍的迭代法是基于把![]() 维问题投影到低维Krylov子空间这一思想.给定矩阵
维问题投影到低维Krylov子空间这一思想.给定矩阵![]() 和向量
和向量![]() ,相联系的Krylov序列是向量
,相联系的Krylov序列是向量![]() 的集合,相应的Krylov子空间是由这些向量顺次组成的集合张成的.
的集合,相应的Krylov子空间是由这些向量顺次组成的集合张成的.
将要讨论的算法可如下表归类:
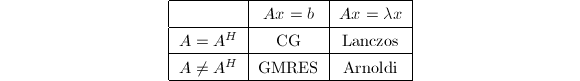 在每一问题中,投影到Krylov子空间的结果是把原来的矩阵问题约化到维数为
在每一问题中,投影到Krylov子空间的结果是把原来的矩阵问题约化到维数为![]() 的矩阵问题的序列.当
的矩阵问题的序列.当![]() 是Hermite矩阵时,约化的矩阵是三对角矩阵.而在非Hermite矩阵情形下,有Hessenberg形式.例如,用Arnoldi方法逼近大矩阵的特征值,是用计算相继较大维数的某些Hessenberg矩阵的特征值完成的.
是Hermite矩阵时,约化的矩阵是三对角矩阵.而在非Hermite矩阵情形下,有Hessenberg形式.例如,用Arnoldi方法逼近大矩阵的特征值,是用计算相继较大维数的某些Hessenberg矩阵的特征值完成的.
 Arnoldi迭代
Arnoldi迭代
Arnoldi迭代是基于以下思想:用正交相似变换把![]() 完全约化到Hessenberg型可记作
完全约化到Hessenberg型可记作![]() ,或
,或![]() .记
.记
![\begin{align*}
Q&=\left[q_1,\cdots,q_n,q_{n+1},\cdots,q_m\right],\\
Q_n&=\left[q_1,\cdots,q_n\right],\\
H&=
\begin{bmatrix}
\tilde{H}_n& *\\
O& *
\end{bmatrix}=
\begin{bmatrix}
H_n& X_1\\
X_2& X_3
\end{bmatrix}.
\end{align*}](./latex/latex2png-IterationMethods_182076805_.gif)
![]() 为
为![]() 的
的![]() 阶子阵,
阶子阵,![]() 为
为![]() 阶顺序主子阵.考察等式的前
阶顺序主子阵.考察等式的前![]() 列,得到
列,得到![]() ,它的第
,它的第![]() 列可以写为
列可以写为![]() 由此,
由此,![]() 为
为![]() 阶Krylov子空间,
阶Krylov子空间,![]() 为一组正交基.
为一组正交基.
由以上关系可以导出,![]() 即
即![]() 在
在![]() 上的投影在基
上的投影在基![]() 上的表示.由此我们可以期望
上的表示.由此我们可以期望![]() 的一些特征值以有效形式与
的一些特征值以有效形式与![]() 的一些特征值有关.
的一些特征值有关.![]() 称为
称为![]() 的Arnoldi特征值估计或
的Arnoldi特征值估计或![]() 关于
关于![]() 的Ritz值.
的Ritz值.
下面给出Arnoldi迭代的算法描述:
若迭代的第![]() 步有
步有![]() ,则迭代中断.但这是一种"良性"的中断,即此时
,则迭代中断.但这是一种"良性"的中断,即此时![]() 的特征值都是
的特征值都是![]() 的特征值.可随机选取正交向量
的特征值.可随机选取正交向量![]() 使迭代进行下去.
使迭代进行下去.
实际分析表明,Arnoldi迭代往往给出![]() 的靠近谱边缘的特征值精确的逼近 (常以几何速度收敛),而这正是实际中感兴趣的情形.
的靠近谱边缘的特征值精确的逼近 (常以几何速度收敛),而这正是实际中感兴趣的情形.
最后指出,Arnoldi迭代同如下的多项式逼近问题之间的联系:
Arnoldi-Lanzcos逼近问题:求![]() 次首一多项式
次首一多项式![]() 使得
使得![]() 为极小值.
为极小值.
有如下定理,其证明可参见[1]:
 GMRES
GMRES
Arnoldi迭代也可用于求解方程组![]() ,其标准算法称为GMRES,是广义极小剩余 (Generalized Minimal Residuals)的简称.
,其标准算法称为GMRES,是广义极小剩余 (Generalized Minimal Residuals)的简称.
GMRES的思想如下:在迭代的第![]() 步,求
步,求![]() 使
使![]() 最小,则
最小,则![]() 的序列将逼近方程组的精确解
的序列将逼近方程组的精确解![]() .特别地,当迭代中止,即
.特别地,当迭代中止,即![]() 的维数小于
的维数小于![]() 时,将有
时,将有![]() ,从而
,从而![]() .
.
由![]() ,存在
,存在![]() 使
使![]() ,从而问题化为求
,从而问题化为求![]() 使
使![]() 最小.由Arnoldi迭代的过程可知,
最小.由Arnoldi迭代的过程可知,![]() 于是在GMRES的第
于是在GMRES的第![]() 步用标准方法 (对
步用标准方法 (对![]() 进行
进行![]() 分解),求得如上问题中的极小化向量
分解),求得如上问题中的极小化向量![]() ,然后令
,然后令![]() .进一步分析指出,由于
.进一步分析指出,由于![]() 的关系,不用对每一个矩阵独立构造
的关系,不用对每一个矩阵独立构造![]() 因子分解,而可以用更新步骤从
因子分解,而可以用更新步骤从![]() 的
的![]() 因子分解来得到
因子分解来得到![]() 的
的![]() 分解,只需要单个Givens旋转和
分解,只需要单个Givens旋转和![]() 工作量.
工作量.
同样指出,GMRES同多项式逼近之间的联系:事实上,我们已经得到GMRES本质上是求常数项为1的不高于![]() 次的多项式
次的多项式![]() ,使
,使![]() 为极小值.
为极小值.
 Lanczos迭代
Lanczos迭代
Lanczos迭代是限定在![]() 是Hermite矩阵情形下的Arnoldi迭代.由于矩阵的对称性,Arnoldi迭代中的Hessenberg矩阵
是Hermite矩阵情形下的Arnoldi迭代.由于矩阵的对称性,Arnoldi迭代中的Hessenberg矩阵![]() 将进而化为三对角矩阵
将进而化为三对角矩阵![]() ,每步迭代的递推式也从
,每步迭代的递推式也从![]() 项减少为
项减少为![]() 项,这使得Lanczos迭代所需的运算更少.
项,这使得Lanczos迭代所需的运算更少.
但舍入误差对Lanczos迭代有着重要的影响.正由于每步迭代仅对三个向量进行正交化,每步的舍入误差导致正交性的损失,从而算法的稳定性降低.实际计算中发现,经过多步迭代后会有所谓"重像 (Ghost)"特征值出现.这些迭代中出现的表观 (而非真实存在)的重特征值与![]() 的实际特征值的重数毫无关系,这些原因使得Lanczos迭代的实用性降低.
的实际特征值的重数毫无关系,这些原因使得Lanczos迭代的实用性降低.
 共轭梯度法 (CG)
共轭梯度法 (CG)
现在假设![]() 不仅是实的和对称的,而且是正定的.在此假设下,由
不仅是实的和对称的,而且是正定的.在此假设下,由![]() 定义的函数
定义的函数![]() 是
是![]() 上的范数,称为
上的范数,称为![]() -范数.共轭梯度迭代在第
-范数.共轭梯度迭代在第![]() 步产生唯一的
步产生唯一的![]() 达到极小这一性质的迭代序列的递推公式系统.
达到极小这一性质的迭代序列的递推公式系统.
下面首先给出CG迭代步骤,之后证明它具有以上所述的极小性质.
由CG迭代的步骤易于归纳地证明该定理.由此,可以得到以下CG迭代的最优性质:
事实上,以上也得到了CG与多项式逼近问题的联系:
求![]() 为常数项为
为常数项为![]() 的不高于
的不高于![]() 次的多项式,使得
次的多项式,使得![]() 为极小值.
为极小值.
 预处理
预处理
矩阵迭代的收敛性依赖于矩阵的性质:特征值,奇异值等.人们发现,在许多情况下,可以对感兴趣的问题加以转换使得矩阵的性质获得巨大的改进."预处理 (preconditioning)"这个过程,对于大多数迭代方法的成功应用是必不可少的.
有多种预处理器可以应用,如对角线缩放式,不完全Cholesky分解等,可以参考[1].
参考文献
[1]数值线性代数, 人民邮电出版社, 2006.
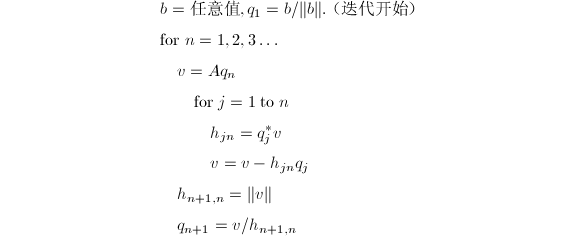 (迭代的每一步计算Krylov子空间的正交基.)
(迭代的每一步计算Krylov子空间的正交基.)
