多项式因子分解问题比最大公因子问题要复杂,因而也更困难一些。然而令人惊喜的是在有限域上,多项式的因子分解问题却变得十分简单,这给我们提供了一种将整数环或有理数域上的多项式因子分解问题转化到较简单的有限域情况上来解决的可能性。
这一部分我们首先解决![]() 域上的多项式因子分解问题。这些内容是
域上的多项式因子分解问题。这些内容是![]() ,
,![]() ,
,![]() 乃至
乃至![]() ,
,![]() 和多元多项式因子分解的基础.
和多元多项式因子分解的基础.
在有限域上进行因子分解的方法很多,一般来说,有限域上多项式因子分解要经过下面三个步骤:
- 无平方因子分解(squarefree factorization)
- 不同次数因子分解(distinct-degree factorization)
- 同次因子分解(equal-degree factorization)
这一章首先将从上面三个方面介绍有限域上的因子分解问题,然后讨论其他算法([1]Chapter 14).
 不同次数因子分解
不同次数因子分解
这里我们假定多项式是无平方因子的(squarefree),即无重因子。这一点很容易做到,比如![]() 含重因子,那么取
含重因子,那么取![]() ,则可消去重因子,得到无重因子的多项式。不同次因子分解(Distinct-degree factorization)即是在无平方因子分解的基础上,将多项式中各不同次数因子的乘积逐一剥离出来。
,则可消去重因子,得到无重因子的多项式。不同次因子分解(Distinct-degree factorization)即是在无平方因子分解的基础上,将多项式中各不同次数因子的乘积逐一剥离出来。
首先我们介绍一些有限域的知识.
 有限域
有限域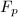 和
和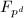
有限域的阶数只可能是素数以及素数的幂,对于![]() ,可以构造
,可以构造![]() 阶的域如下:
阶的域如下:![]() 其中
其中![]() 是
是![]() 次不可约多项式。
次不可约多项式。
Fermat小定理![]() 对于素数以及素数的幂均成立,素数的幂情况证明同素数情况。
对于素数以及素数的幂均成立,素数的幂情况证明同素数情况。
下面的定理是Fermat小定理的推广,Fermat小定理是其![]() 的特殊情形。
的特殊情形。
若![]() ,则由Fermat小定理,可以取
,则由Fermat小定理,可以取![]() 的子集
的子集![]() 使得
使得![]() .任取
.任取![]() ,令
,令![]() ,其中
,其中![]() 是
是![]() 中包含
中包含![]() 的最小子域,有
的最小子域,有![]() 个元素,
个元素,![]() 是它的扩域,因此
是它的扩域,因此![]() .
.
若![]() ,令
,令![]() ,且
,且![]() 为
为![]() 的一个根。而
的一个根。而![]() ,由于
,由于![]() ,设
,设![]() 则
则![]() 将上式乘以
将上式乘以![]() 则可得
则可得![]() .因此在
.因此在![]() 中
中![]() ,由于
,由于![]() 中多项式的最大公因子应该也在
中多项式的最大公因子应该也在![]() 中,于是由其非平凡可推出
中,于是由其非平凡可推出![]() ,即
,即![]() .
□
.
□
 不同次因子分解算法
不同次因子分解算法
不同次因子分解算法即是要求出多项式的不同次因子序列,其定义如下:
显然![]() 成立,设
成立,设![]() 均成立,则对
均成立,则对![]() ,有
,有![]() 且
且![]()
由Fermat小定理推广,![]() 是
是![]() 中所有首一不可约且次数整除
中所有首一不可约且次数整除![]() 的多项式的乘积且能整除
的多项式的乘积且能整除![]() ,因此
,因此![]() (低于
(低于![]() 次的因子已在前面提出了).于是归纳证明了
次的因子已在前面提出了).于是归纳证明了![]() 成立,也同时可得
成立,也同时可得![]() .
□
.
□
算法1可在![]() 时即终止,因为
时即终止,因为![]() 所有不可约因子次数至少为
所有不可约因子次数至少为![]() ,因此
,因此![]() 即已经是不可约的了。
即已经是不可约的了。
 同次因子分解
同次因子分解
本节基于上一节不同次因子分解的结果继续对其进行同次因子分解(Equal-degree factorization),或者Cantor-Zassenhaus算法,直到将![]() 完全分解为不可约多项式的积。但是由于奇素数与2在下面的处理技术中有一点微小的区别,因此本节分成两部分来讨论.
完全分解为不可约多项式的积。但是由于奇素数与2在下面的处理技术中有一点微小的区别,因此本节分成两部分来讨论.
 特征为奇素数的有限域
特征为奇素数的有限域
![]() 对于任何
对于任何![]() 均成立,由Fermat小定理得
均成立,由Fermat小定理得![]() ,则
,则![]() .于是由群同态定理
.于是由群同态定理
![]() 则
则![]() 且
且![]() ,
,![]() .
□
.
□
作为上面引理的推论,我们有
下面的概率性算法给出![]() 的可能因子,其中
的可能因子,其中![]() 是经上节算法给出的无平方首一同次因子乘积,即存在
是经上节算法给出的无平方首一同次因子乘积,即存在![]() 的一个因子
的一个因子![]() 使得
使得![]() 可分解为
可分解为![]() 个
个![]() 次首一不可约因子.
次首一不可约因子.
输入:![]() ,
,![]() ,
,
输出:![]() 的首一因子
的首一因子![]() ,或者failure.
,或者failure.
- (随机)任取
![$a\in\mathbb{F}_q[x]$](./latex/latex2png-PolyFacZp_213602218_-5.gif) 使得
使得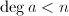 .若
.若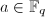 则输出failure,
则输出failure, 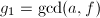 ,若
,若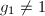 且
且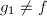 则输出
则输出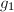 ,
,- 调用快速求幂算法在环
![$R=\mathbb{F}_q[x]/\langle f\rangle$](./latex/latex2png-PolyFacZp_148078825_-5.gif) 中计算
中计算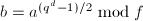 ,
, 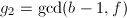 ,若
,若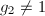 且
且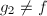 则输出
则输出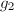 ,否则输出failure.
,否则输出failure.
若设![]() ,则由中国剩余定理有如下的环同构:
,则由中国剩余定理有如下的环同构:
![]() 其中
其中![]() .
引入下面记号:
.
引入下面记号:![]() ,其中
,其中![]() .记
.记![]() ,则对任意
,则对任意![]() ,我们有
,我们有![]() ,且取两个值是等概率的.如果我们随机任意选取
,且取两个值是等概率的.如果我们随机任意选取![]() 使得
使得![]() 且
且![]() ,则
,则![]() 是
是![]() 中随机元素,且
中随机元素,且![]() 等概率取
等概率取![]() 或
或![]() ,因此
,因此![]() 此时
此时![]() 是
是![]() 的一个因子(不一定不可约),除非
的一个因子(不一定不可约),除非![]() (若有
(若有![]() 则
则![]() ,则
,则![]() .),而后一种情况发生的概率为
.),而后一种情况发生的概率为![]() .(
.(![]() )
)
 特征为2的有限域
特征为2的有限域
以下设![]() 是一特征为2的域,且
是一特征为2的域,且![]() ,
,![]() 是一正整数.
是一正整数.![]() 上多项式
上多项式![]() 是无平方因子
是无平方因子![]() 次多项式,且是
次多项式,且是![]() 个
个![]() 次不可约多项式之积.
次不可约多项式之积.
 一个完整的因子分解算法
一个完整的因子分解算法
对于有重因子的多项式![]() ,利用上两节的方法可以完全将其分解。如果设
,利用上两节的方法可以完全将其分解。如果设![]() 是首一的,并且
是首一的,并且![]() 的首一不可约因子分解为
的首一不可约因子分解为![]() ,记
,记![]() 表示它的分解,则可利用下面的算法给出此分解:
表示它的分解,则可利用下面的算法给出此分解:
输入:首一多项式![]() ,
,![]() 为一素数幂.
为一素数幂.
输出:![]() 的分解
的分解![]() .
.
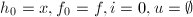 ,
,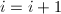 ,
,- 不同次因子分解:利用快速求幂算法计算
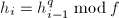 ,
,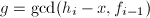 ,
, - 若
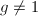 则利用算法3求出
则利用算法3求出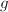 的所有同次首一不可约因子
的所有同次首一不可约因子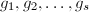 ,
, 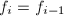 ,并不断除以
,并不断除以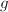 的同次因子求出
的同次因子求出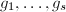 的次数
的次数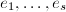 ,每求出一个
,每求出一个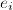 ,将
,将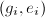 添入
添入 ,
,- 直至
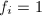 ,否则转第2步,
,否则转第2步, - 输出
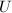 .
.
作为前面提过的诸多因子分解算法的应用,下面讨论多项式求根问题。设![]() 为
为![]() 上一非平凡多项式,则下面的算法给出其所有
上一非平凡多项式,则下面的算法给出其所有![]() 中的根。
中的根。
这样算法就避免了将![]() 完全分解,先将其与
完全分解,先将其与![]() 取最大公因子,使得结果只能含有形如
取最大公因子,使得结果只能含有形如![]() 的因子。由此而衍生出下面的
的因子。由此而衍生出下面的![]() 中求整数根的算法,但在引入该算法之前,先有下面的:
中求整数根的算法,但在引入该算法之前,先有下面的:
于是![]() .
□
.
□
若![]() ,则显然有
,则显然有![]() .可设
.可设![]() ,则由引理4知
,则由引理4知![]() .但由于
.但由于![]() ,且两边多项式系数均比
,且两边多项式系数均比![]() 小,则有
小,则有![]() ,故也有
,故也有![]() .
.
另一方面,若![]() 且
且![]() ,则
,则![]() ,因此
,因此![]()
证毕。 □
 无平方因子分解
无平方因子分解
这一小节详细介绍无平方因子分解(Squarefree factorization).我们分两个部分进行.
 特征为零的域上无平方分解
特征为零的域上无平方分解
我们先假定![]() 是一特征为零的域,那么我们已经知道若
是一特征为零的域,那么我们已经知道若![]() 是
是![]() 的
的![]() 阶零点,则其是
阶零点,则其是![]() 的
的![]() 阶零点,于是
阶零点,于是![]() 中将只含
中将只含![]() 的一次因子。当然我们可以在
的一次因子。当然我们可以在![]() 的代数扩域上证明若
的代数扩域上证明若![]() 是
是![]() 的一个不可约因子,那么
的一个不可约因子,那么![]() ,但我们也可以在任一域
,但我们也可以在任一域![]() 内证明如下的命题:
内证明如下的命题:
有了上面的定理,则首先我们可以在特征为零的域上求出![]() 的无平方因子部分(squarefree part).
的无平方因子部分(squarefree part).
还有一种无平方分解的算法,即若首一非平凡多项式![]() ,其中
,其中![]() 两两互素且无平方因子,
两两互素且无平方因子,![]() ,则称
,则称![]() 为
为![]() 的无平方分解(squarefree decompositon).在特征非零的域
的无平方分解(squarefree decompositon).在特征非零的域![]() 上有如下一种较快的分解算法。
上有如下一种较快的分解算法。
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
最后输出![]() .
.
 特征有限的域上无平方分解
特征有限的域上无平方分解
我们再来考虑特征有限的域上无平方分解。我们已经看到在有限域上,例如素域![]() 中,与特征为零的域的区别为对于一个非平凡的多项式
中,与特征为零的域的区别为对于一个非平凡的多项式![]() ,它的形式微商仍然可能是零。下面探讨一下什么情况下形式微商为零,以及此时的多项式有什么特点。
,它的形式微商仍然可能是零。下面探讨一下什么情况下形式微商为零,以及此时的多项式有什么特点。
考虑多项式![]() ,
,![]() 是一素数.若其微商为零,则
是一素数.若其微商为零,则![]() ,若
,若![]() ,则须有
,则须有![]() ,于是
,于是![]() 中所含的单项均是
中所含的单项均是![]() 的
的![]() 的倍数的幂次项,亦即
的倍数的幂次项,亦即![]() .于是:
.于是: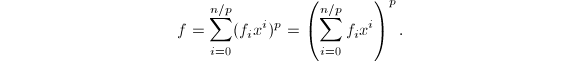 则
则![]() 是一个
是一个![]() 次幂,对于素幂阶的域
次幂,对于素幂阶的域![]() ,也有下面的结论:
,也有下面的结论:
由上面的定理我们知道不可约非平凡多项式的形式微商一定非零。现在前面的算法唯一不可行之处即是对于![]() 的情形。设
的情形。设![]() ,式中
,式中![]() 两两互素且不可约,
两两互素且不可约,![]() ,
,![]() 均是正整数.显然我们有
均是正整数.显然我们有![]() 则
则![]() ,于是
,于是![]() 其中缺少了某些项,这些项的次数均是
其中缺少了某些项,这些项的次数均是![]() 的倍数.
的倍数.
我们注意到多项式![]() 中含有我们需要的这些幂次,且
中含有我们需要的这些幂次,且![]() ,则有如下关系:
,则有如下关系:![]()
![]() 为
为![]() 次幂。由此我们可以得到如下算法:
次幂。由此我们可以得到如下算法:
递归调用算法,计算![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
再次递归调用的结果为![]() .
.
故最后输出![]() .
.
上节中的例4给了我们对于算法9的理解:![]() 序列包含了要处理的无平方部分,
序列包含了要处理的无平方部分,![]() ,
,![]() ,
,![]() 是
是![]() 在
在![]() 中的次数(在下面的说明中
中的次数(在下面的说明中![]() ),每处理一次,
),每处理一次,![]() 中去掉次数
中去掉次数![]() 的项,如果是在有限域中,该算法就只能在
的项,如果是在有限域中,该算法就只能在![]() 时正确,因为它会将模
时正确,因为它会将模![]() 相同的次数归于同一个次数(小于
相同的次数归于同一个次数(小于![]() 的那个)。即会有下面的结果:
的那个)。即会有下面的结果:![]()
![]()
假设![]() ,
,![]() ,则算出
,则算出![]() 后,令
后,令![]() ,则
,则
![]() 于是
于是
![]()
如果我们能够构造递归算法以得到![]() 的无平方分解
的无平方分解![]() ,则显然有
,则显然有
![]() 于是
于是![]() .
.
上面给我们提供了一种利用递归进行分解的想法:
 Berlekamp 算法
Berlekamp 算法
最早的多项式时间的算法是Berlekamp于1967至1970年间提出的.为了引入这个算法,我们有必要在此讨论一些代数问题.
 Frobenius映射和Berlekamp子代数
Frobenius映射和Berlekamp子代数
以下设![]() 是一首一无平方因子多项式,
是一首一无平方因子多项式,![]() 且
且![]() ,
,![]() 为两两互素且不可约首一多项式.由中国剩余定理有下面的环同构:
为两两互素且不可约首一多项式.由中国剩余定理有下面的环同构:![]() 并定义同构映射:
并定义同构映射:![]()
又由于![]() ,则
,则![]() 是满射,因而是同构.
□
是满射,因而是同构.
□
于是![]() .而显然后者也属于前者,于是有两者相等,
.而显然后者也属于前者,于是有两者相等,![]() .
□
.
□
取![]() 的一组基
的一组基![]() ,因为
,因为![]() ,可设这组基在
,可设这组基在![]() 中的表示矩阵为
中的表示矩阵为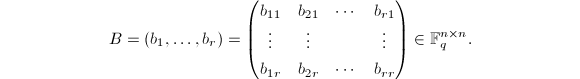
此为一可逆矩阵,于是![]() ,
,![]() 使得
使得![]() ,即
,即![]() ,则对于
,则对于![]() 有
有![]()
则![]() 是可以分离
是可以分离![]() 的一个多项式.
的一个多项式.
 Berlekamp算法的实现
Berlekamp算法的实现
有了上面的准备工作,下面我们可以来引入Berlekamp算法了.
输入:![]() 上无平方因子首一
上无平方因子首一![]() 次非平凡多项式
次非平凡多项式![]() ,
,
输出:![]() 可能的非平凡因子,或者失败.
可能的非平凡因子,或者失败.
- 构作环
![$R=\field{q}[x]/\idea{f}$](./latex/latex2png-PolyFacZp_229169362_-5.gif) 上的Frobenius映射的表示矩阵
上的Frobenius映射的表示矩阵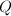 ,即Petr-Berlekamp矩阵,
,即Petr-Berlekamp矩阵, - 对
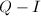 进行高斯消元法,求出
进行高斯消元法,求出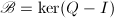 的
的 个基矢,
个基矢,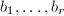 ,
, - 随机任取一个基矢
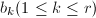 ,任取
,任取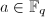 ,对
,对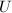 中任何一个元素
中任何一个元素 ,计算
,计算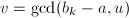 ,若
,若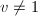 且
且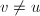 ,则输出
,则输出 ,否则输出失败.
,否则输出失败.
下面是另外一种概率性的Berlekamp算法,能给出![]() 的可能因子.
的可能因子.
输出:![]() 的可能非平凡因子,或者失败.
的可能非平凡因子,或者失败.
- 构作环
![$R=\field{q}[x]/\idea{f}$](./latex/latex2png-PolyFacZp_229169362_-5.gif) 上的Petr-Berlekamp矩阵Q,
上的Petr-Berlekamp矩阵Q, - 对
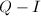 进行高斯消元法,求出
进行高斯消元法,求出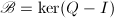 的
的 个基矢
个基矢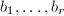 ,
, - 随机任取互相独立的
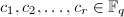 ,计算
,计算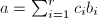 ,
, 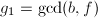 ,若
,若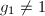 且
且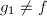 则输出
则输出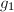 ,
,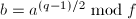 ,
,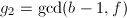 ,
,- 若
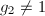 且
且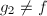 则输出
则输出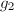 ,否则输出失败.
,否则输出失败.
该算法的正确性证明与奇素数幂同次因子分解类似,只须注意到![]() ,这样我们有
,这样我们有![]() ,两种取值等概率为
,两种取值等概率为![]() .
.
为了引入特征为2的域上与算法13对应的Berlekamp算法,我们先回忆定义2中对![]() 阶迹多项式(mth trace polynoial)
阶迹多项式(mth trace polynoial)![]() 的定义.
的定义.
易知,当且仅当![]() 时,
时,![]() 含有
含有![]() 的非平凡因子.
□
的非平凡因子.
□
于是对于特征为2的域![]() ,有如下的:
,有如下的:
有限域上的因子分解算法在近些年有很多进展,如1998年Kaltofen和Shoup的Subquadratic算法(见[2]),Huang和Pan的Fast rectangular matrix multiplication算法(见[3])等等.
 素性检测和不可约多项式的构造
素性检测和不可约多项式的构造
若要检测一个多项式的不可约性,前面的因子分解的方法当然也是适用的,只需相应修改算法终止即可,下面再介绍一个比较简单的检测方法.
输入:![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 首一且不为零,
首一且不为零,
输出:![]() .
.
![$m=[n^{1/2}]$](./latex/latex2png-PolyFacZp_253806728_-5.gif) ,并设
,并设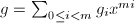 ,其中
,其中![$g_0,\ldots,g_{m-1}\in R[x]$](./latex/latex2png-PolyFacZp_181751577_-5.gif) 的次数少于
的次数少于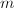 ,
,- 对于
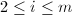 ,计算
,计算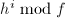 ,
, - 令
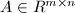 ,其行由
,其行由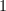 ,
,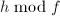 ,
,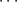 ,
,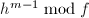 的系数组成,
的系数组成,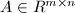 ,其行由
,其行由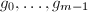 的系数组成,计算
的系数组成,计算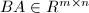 ,
, - 对于
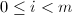 循环,令
循环,令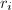 为
为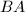 第
第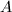 行作为系数构成的多项式,并计算
行作为系数构成的多项式,并计算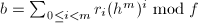 (利用Horner规则),
(利用Horner规则), - 输出b.
构造一个不可约多项式的最基本的想法就是随机取一个多项式,再对其作素性检测。于是我们必须要对随机选取取到不可约多项式的概率进行估计。首先我们有下面的引理:
参考文献
[1]Modern Computer Algebra, Cambridge University Press, 2002.
[2]Subquadratic-Time Factoring of Polynomials over Finite Fields, Mathematics of Computation 67 (1998), 1179-1197.
[3]Fast Rectangular Matrix Multiplication and Applications, Journal of Complexity 14 (1998), 257-299.
[4]初等数论及应用, 北京师范大学出版社, 北京, 2003.
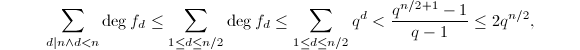 因此
因此